
【题目】如图,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 垂直平分线段
垂直平分线段 ![]() ,分别交
,分别交![]() 、
、 ![]() 、
、![]() 延长线于点
延长线于点![]() 、
、![]() 、
、![]() ,则下列结论: ①
,则下列结论: ①![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() .其中正确的结论是__________.(填写所有正确结论的序号)
.其中正确的结论是__________.(填写所有正确结论的序号)
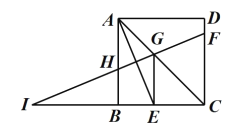
【答案】①②③
【解析】
:①在△AOH和△BIH中,根据三角形内角和定理,如图两个角对应相等,则第三个角∠FIB=∠BAE=22.5°;
②根据线段中垂线定理证明∠AEG=∠EAG=22.5°=∠BAE,可得EG∥AB;
③根据等量代换可得:∠CGF=∠BHI,可作判断;
④连接EH,证明四边形AHEG是菱形,根据EH>BH,及相似三角形的性质可作判断.
解:①如图,∵四边形ABCD是正方形,
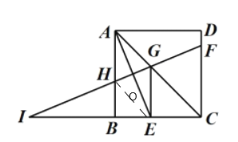
∴∠BAC=![]() ∠BAD=45°,
∠BAD=45°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=22.5°,
∵IF是AE的中垂线,
∴AE⊥PQ,
∴∠AOH=90°,
∵∠AOH=∠HBI=90°,∠AHO=∠IHB,
∴∠FIB=∠BAE=22.5°;
故①正确;
②∵OG是AE的中垂线,
∴AG=EG,
∴∠AEG=∠EAG=22.5°=∠BAE,
∴EG∥AB,
故②正确;
③∵∠HAO=∠GAO,∠AOH=∠AOG=90°,
∴∠AHO=∠AGO,
∵∠CGF=∠AGO,∠BHI=∠AHO,
∴∠CGF=∠BHI,
在Rt△BHI中,tan∠CGF=tan∠BHI=![]() ,
,
故③正确;
④连接EH,
∵AH=AG=EG,EG∥AB,
∴四边形AHEG是菱形,
∴AH=EH=EG>BH,
∴![]() ≠
≠![]() ,
,
∵EG∥AB,
∴△CEG∽△CBA,
∴![]() =(
=(![]() )2≠
)2≠![]() ,
,
故④不正确;
本题正确的是:①②③,
故答案是:①②③.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点(不与端点重合),将
边上一点(不与端点重合),将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
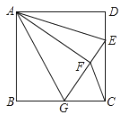
①![]() __________;
__________;
②若![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
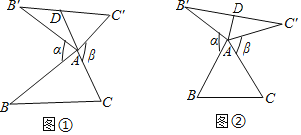
【题目】如图①,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的旋补三角形,△AB′C′边B′C′上的中线AD叫做△ABC的旋补中线.
如图②,当△ABC为等边三角形时,△AB′C′是△ABC的旋补三角形,AD是旋补中线,AD与BC的数量关系为:AD=_____BC;当BC=8时,则B′C′长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,E为BC的中点.将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则△CDF的面积为( )
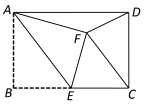
A. 3.6 B. 4.32 C. 5.4 D. 5.76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为 .
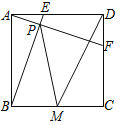
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则△PMN周长的最小值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中线,过点D作
的中线,过点D作![]() 于点E,延长
于点E,延长![]() 至点F,使
至点F,使![]() ,连接
,连接![]() ,点G在线段
,点G在线段![]() 上,连接
上,连接![]() ,且
,且![]() .下列结论:①
.下列结论:①![]() ;②四边形
;②四边形![]() 是平行四边形;③
是平行四边形;③![]() ;④
;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
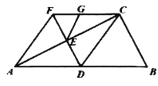
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题解答]
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
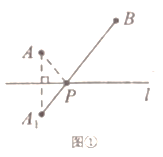
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
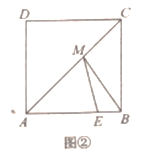
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
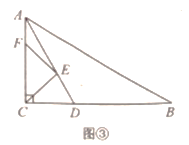
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在
在![]() 上.则下列命题为真命题的是( )
上.则下列命题为真命题的是( )
A.若半径![]() 平分弦
平分弦![]() .则四边形
.则四边形![]() 是平行四边形
是平行四边形
B.若四边形![]() 是平行四边形.则
是平行四边形.则![]()
C.若![]() .则弦
.则弦![]() 平分半径
平分半径![]()
D.若弦![]() 平分半径
平分半径![]() .则半径
.则半径![]() 平分弦
平分弦![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com