
【题目】在平面直角坐标系中,点![]() ,
,![]() ,点C为x轴正半轴上一动点,过点A作
,点C为x轴正半轴上一动点,过点A作![]() 交y轴于点E.
交y轴于点E.
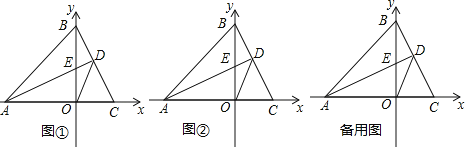
![]() 如图
如图![]() ,若点C的坐标为
,若点C的坐标为![]() ,试求点E的坐标;
,试求点E的坐标;
![]() 如图
如图![]() ,若点C在x轴正半轴上运动,且
,若点C在x轴正半轴上运动,且![]() , 其它条件不变,连接DO,求证:OD平分
, 其它条件不变,连接DO,求证:OD平分![]()
![]() 若点C在x轴正半轴上运动,当
若点C在x轴正半轴上运动,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)∠OCB=60°.
【解析】
(1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(2,0),得到OC=2=OE,进而得到点E的坐标;
(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD平分∠ADC;
(3)在DA上截取DP=DC,连接OP,根据SAS判定△OPD≌△OCD,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°.
(1)如图①,∵AD⊥BC,BO⊥AO,
∴∠AOE=∠BDE,
又∵∠AEO=∠BED,
∴∠OAE=∠OBC,
∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOE≌△BOC,
∴OE=OC,
又∵点C的坐标为(2,0),
∴OC=2=OE,
∴点E的坐标为(0,2);
(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,

∵△AOE≌△BOC,
∴S△AOE=S△BOC,且AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC;
(3)如所示,在DA上截取DP=DC,连接OP,

∵∠PDO=∠CDO,OD=OD,
∴△OPD≌△OCD,
∴OC=OP,∠OPD=∠OCD,
∵AD-CD=OC,
∴AD-DP=OP,即AP=OP,
∴∠PAO=∠POA,
∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB,
又∵∠PAO+∠OCD=90°,
∴3∠PAO=90°,
∴∠PAO=30°,
∴∠OCB=60°.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE.以点A为原点,分别以AD所在的直线为x轴,AB所在的直线为y轴建立坐标系.
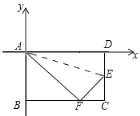
(1)写出点B、D、E、F的坐标;
(2)在坐标轴上是否存在点G,使△AFG是以AF为腰长的等腰三角形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题.
(1)![]()
(2)![]()
(3)2002-202×198
(4)![]()
(5)[(2x+y)2﹣y(y+4x)﹣8xy]÷(﹣2x).其中x=-2,y=1
查看答案和解析>>
科目:初中数学 来源: 题型:
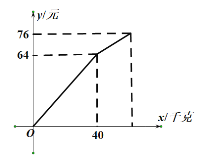
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C在线段BE上,分别以BC、CE为边作等边三角形ABC和等边三角形DCE,连接AE与CD相交于点N,连接BD与AC相交于点M,连接OC、MN,则以下结论①AE=BD;②△ACN≌△BCM;③∠BOE=120°;④△MNC是等边三角形;⑤OC平分∠BOE;正确的个数是( )
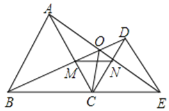
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
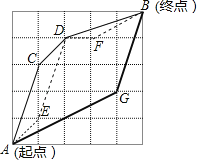
【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为:A(-1,2),B(-2,-1),C(2,0).
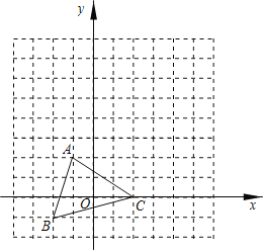
(1)作图:将△ABC先向右平移4个单位,再向上平移3个单位,则得到△A1B1C1,作出△A1B1C1;(不要求写作法)
(2)写出下列点的坐标:A1______;B1______;C1______.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
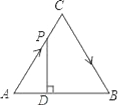
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
A.  B.
B.  C.
C. 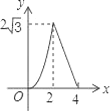 D.
D. 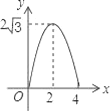
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com