Question

【题目】如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：
①∠AOB=90°+ ∠C；
②AE+BF=EF；
③当∠C=90°时，E，F分别是AC，BC的中点；
④若OD=a，CE+CF=2b，则S△CEF=ab．
其中正确的是（ ）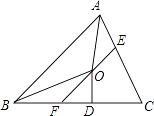

A.①②
B.③④
C.①②④
D.①③④

Answer 1

【答案】C
【解析】解：∵∠BAC和∠ABC的平分线相交于点O，
∴∠OBA= ∠CBA，∠OAB= ∠CAB，
∴∠AOB=180°﹣∠OBA﹣∠OAB
=180°﹣ ∠CBA﹣ ∠CAB
=180°﹣ （180°﹣∠C）
=90°+ ∠C，①正确；
∵EF∥AB，
∴∠FOB=∠ABO，又∠ABO=∠FBO，
∴∠FOB=∠FBO，
∴FO=FB，
同理EO=EA，
∴AE+BF=EF，②正确；
当∠C=90°时，AE+BF=EF＜CF+CE，
∴E，F分别是AC，BC的中点，③错误；
作OH⊥AC于H，
∵∠BAC和∠ABC的平分线相交于点O，
∴点O在∠C的平分线上，
∴OD=OH，
∴S△CEF= ×CF×OD ×CE×OH=ab，④正确．
故选：C．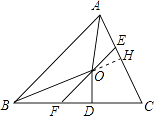

【考点精析】本题主要考查了平行线的性质和角平分线的性质定理的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．