
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由点A的坐标结合反比例函数系数k的几何意义,即可求出m的值;
(2)设点B的坐标为(n,![]() ),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
试题解析:(1)∵点A(4,1)在反比例函数![]() 的图象上,∴m=4×1=4,∴反比例函数的解析式为
的图象上,∴m=4×1=4,∴反比例函数的解析式为![]() .
.
(2)∵点B在反比例函数![]() 的图象上,∴设点B的坐标为(n,
的图象上,∴设点B的坐标为(n,![]() ).
).
将y=kx+b代入![]() 中,得:
中,得:
kx+b=![]() ,整理得:
,整理得:![]() ,∴4n=
,∴4n=![]() ,即nk=﹣1①.
,即nk=﹣1①.
令y=kx+b中x=0,则y=b,即点C的坐标为(0,b),∴S△BOC=![]() bn=3,∴bn=6②.
bn=3,∴bn=6②.
∵点A(4,1)在一次函数y=kx+b的图象上,∴1=4k+b③.
联立①②③成方程组,即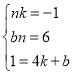 ,解得:
,解得: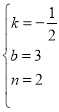 ,∴该一次函数的解析式为
,∴该一次函数的解析式为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+ ![]() ∠C;
∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )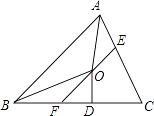
A.①②
B.③④
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,反比例函数![]() 的图象过点A(
的图象过点A(![]() ,2).
,2).
(1)求k的值;
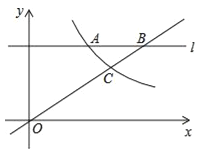
(2)如图,在反比例函数![]() (x>0)上有一点C,过A点的直线l∥x轴,并与OC的延长线交于点B,且OC=2BC,求点C的坐标.
(x>0)上有一点C,过A点的直线l∥x轴,并与OC的延长线交于点B,且OC=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
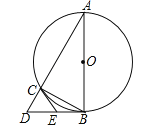
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.坐标平面内的点与有序数对是一一对应的
B.在x轴上的点纵坐标为零
C.在y轴上的点横坐标为零
D.平面直角坐标系把平面上的点分为四部分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com