
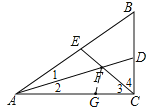
【题目】如图①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
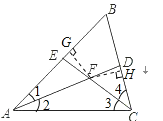
(2)如图②,如果∠ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

【答案】(1)FE=FD (2)答案见解析
【解析】
(1)先在AC上截取AG=AE,连结FG,利用SAS判定△AEF≌△AGF,得出∠AFE=∠AFG,FE=FG,再利用ASA判定△CFG≌△CFD,得到FG=FD,进而得出FE=FD;
(2)先过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,根据已知条件得到∠GEF=∠HDF,进而判定△EGF≌△DHF(AAS),即可得出FE=FD.也可以过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,再判定△EFG≌△DFH(ASA),进而得出FE=FD.
(1)FE与FD之间的数量关系为:FE=FD.
理由:如图,在AC上截取AG=AE,连结FG,
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△AEF与△AGF中
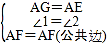 ,
,
∴△AEF≌△AGF(SAS),
∴∠AFE=∠AFG,FE=FG,
∵∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,
∴2∠2+2∠3+∠B=180°,
∴∠2+∠3=60°,
又∵∠AFE为△AFC的外角,
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°,
∴∠CFG=180°-60°-60°=60°,
∴∠GFC=∠DFC,
在△CFG与△CFD中,
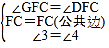 ,
,
∴△CFG≌△CFD(ASA),
∴FG=FD,
∴FE=FD;
(2)结论FE=FD仍然成立.
如图,过点F分别作FG⊥AB于点G,FH⊥BC于点H,则∠FGE=∠FHD=90°,
∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=∠1+∠2+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH,
又∵∠HDF=∠B+∠1=60°+∠1,
∴∠GEF=∠HDF,
在△EGF与△DHF中,
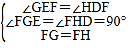 ,
,
∴△EGF≌△DHF(AAS),
∴FE=FD.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 为等边三角形,
为等边三角形,![]()
![]() ,垂足为点
,垂足为点![]() .
.![]()
![]() ,垂足为
,垂足为![]() .
.

(1)求OF的长;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() 交
交![]() 于E,求OE的长.
于E,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
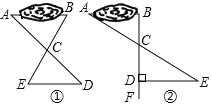
方案1:如图(1),先在平地上取一个可以直接到达A、B的点C,连接AC并延长AC至点D,连接BC并延长至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长.
方案2:如图(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB间的距离
问:(1)方案1是否可行?并说明理由;
(2)方案2是否可行?并说明理由;
(3)小明说:“在方案2中,并不一定需要BF⊥AB,DE⊥BF,将“BF⊥AB,DE⊥BF”换成条 也可以.”你认为小明的说法正确吗?如果正确的话,请你把小明所说的条件补上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,![]() 、
、![]() 、
、![]() 在同一条直线上,连接
在同一条直线上,连接![]() .
.

(1)请找出图2中的全等三角形,并说明理由(说明:结论中不得含有图中未标识的字母);
(2)![]() 与
与![]() 垂直吗?为什么?
垂直吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+![]() x+2与直线y=
x+2与直线y=![]() x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
(1)求点C和D的坐标;
(2)求抛物线与x轴的交点坐标;
(3)如果以P、C、O、F为顶点的四边形是平行四边形,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
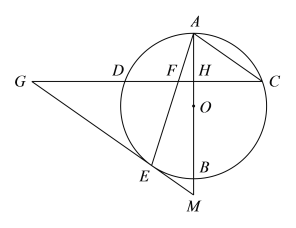
(1)求证:EG是⊙O的切线;
(2)延长AB交GE的延长线于点M,若AH=2,![]() ,求OM的长.
,求OM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com