Question

【题目】如图，在平面直角坐标系中，，点在第一象限，为等边三角形，，垂足为点．，垂足为．

（1）求OF的长；

（2）作点关于轴的对称点，连交于E，求OE的长．

Answer 1

【答案】（1）6；（2）2.

【解析】

（1）先过点B作BH⊥OA，垂足为F．由等腰三角形三线合一的性质可知OF＝AF＝4、BC＝AC，根据等边三角形的性质可得：∠BOF＝60°，根据特殊锐角三角函数值可得FB＝，从而得到点B的坐标为（4，），再根据中点坐标公式可得点C的坐标为（6，），从而得到OF的长度；
（2）连接CD，交OB于G．由关于y轴对称的点的坐标特点可知：CD∥OA，D（6，），从而得到DC＝12，由题意可知△BCG为等边三角形，从而得到CG＝4，然后可求得DG＝124＝8＝OA，依据AAS可证明△DEG≌△AEO，由全等三角形的性质可知OE＝EG，从而求得OE的长度．

解：（1）如图所示：过点B作BH⊥OA，垂足为H．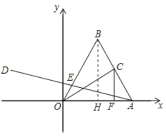

∵OB＝AB，BH⊥OA，
∴OH＝AH＝4．
∵△OAB为等边三角形，
∴∠BOH＝60°．
∴HB＝OBsin60°＝8×＝．
∴点B的坐标为（4，）．
∵AO＝OB，OC⊥AB，
∴BC＝AC．
由中点坐标公式可知点C的坐标为（6，）．
∴OF＝6；
（2）如图所示：连接CD，交OB于G．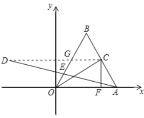

∵点C与点D关于y轴对称，
∴CD∥OA，点D（6，）．
∴△BCG为等边三角形，
∴CG＝4，CD＝12．
∴DG＝124＝8＝OA．
在△DEG和△AEO中，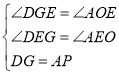

∴△DEG≌△AEO（AAS），
∴OE＝EG＝OG，
∵BG＝BC＝4，
∴OG＝4，
∴OE＝2．