
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB=![]() ,BE=
,BE=![]() ,求PF的长.
,求PF的长.

【答案】(1)见解析;(2)PC=PF.证明见解析;(3)![]() .
.
【解析】试题分析:(1)、连接OC,根据切线的性质得出∠OCP=∠D=90°即 OC∥AD,然后根据OA=OC得出∠CAD=∠OCA=∠OAC,从而得出角平分线;(2)、根据∠PCB+∠ACD=∠CAD+∠ACD=90°,从而得出∠CAB=∠CAD=∠PCB,结合∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE得出∠PFC=∠PCF,从而得出答案;(3)、连接AE,根据题意得出△PCB和△PAC相似,然后设PB=3x,则PC=4x,根据Rt△POC的勾股定理得出x的值,从而得出答案.
试题解析:(1)连接OC. ∵OA=OC,∴∠OAC=∠OCA.
∵PC是⊙O的切线,AD⊥CD, ∴∠OCP=∠D=90°, ∴ OC∥AD.
∴ ∠CAD=∠OCA=∠OAC.即AC平分∠DAB.
(2)PC=PF.
证明:∵AB是直径, ∴∠ACB=90°,∴∠PCB+∠ACD=90° 又∵∠CAD+∠ACD=90°,
∴∠CAB=∠CAD=∠PCB.
又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE. ∴∠PFC=∠PCF.
∴PC=PF.
(3)连接AE. ∵∠ACE=∠BCE,∴![]() =
=![]() , ∴AE=BE.
, ∴AE=BE.
又∵AB是直径, ∴∠AEB=90°.AB=![]() , ∴OB=OC=5.
, ∴OB=OC=5.
∵∠PCB=∠PAC,∠P=∠P, ∴△PCB∽△PAC. ∴![]() .
.
∵tan∠PCB=tan∠CAB=![]() , ∴
, ∴![]() =
=![]() .
.
设PB=3x,则PC=4x,在Rt△POC中,(3x+5)2=(4x)2+52,
解得x1=0,![]() . ∵x>0,∴
. ∵x>0,∴![]() , ∴PF=PC=
, ∴PF=PC=![]() .
.



 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 为等边三角形,
为等边三角形,![]()
![]() ,垂足为点
,垂足为点![]() .
.![]()
![]() ,垂足为
,垂足为![]() .
.

(1)求OF的长;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() 交
交![]() 于E,求OE的长.
于E,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
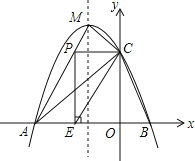
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点
与x轴交于A、B两点,与y轴交于点![]() ,且此抛物线的顶点坐标为
,且此抛物线的顶点坐标为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 设点D为已知抛物线对称轴上的任意一点,当
设点D为已知抛物线对称轴上的任意一点,当![]() 与
与![]() 面积相等时,求点D的坐标;
面积相等时,求点D的坐标;
![]() 点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将
点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将![]() 沿直线CE翻折,使点P的对应点
沿直线CE翻折,使点P的对应点![]() 与P、E、C处在同一平面内,请求出点
与P、E、C处在同一平面内,请求出点![]() 坐标,并判断点
坐标,并判断点![]() 是否在该抛物线上.
是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,以点![]() 为直角顶点,
为直角顶点,![]() 为腰在
为腰在![]() 右侧作等腰
右侧作等腰![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
(2)如图②,以![]() 为底边在
为底边在![]() 左侧作等腰
左侧作等腰![]() ,连接
,连接![]() ,求
,求![]() 的度数.
的度数.
(3)如图③,![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,以
,以![]() 为边在
为边在![]() 左侧作等边
左侧作等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,若AB∥CD,求∠B+∠D+∠E1的度数?
(2)如图②,若AB∥CD,求∠B+∠D+∠E1+∠E2的度数?
(3)如图③,若AB∥CD,求∠B+∠D+∠E1+∠E2+∠E3的度数?
(4)如图④,若AB∥CD,猜想∠B+∠D+∠E1+∠E2+…+∠En的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() .
.

(1)若![]() 为线段
为线段![]() 上的一个点,过点
上的一个点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]()
①若![]() ,
,![]() ,则
,则![]()
![]() ;
;
②猜想![]() 与
与![]() 、
、![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
(2)若![]() 在线段
在线段![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .请你做出示意图,直接写出
.请你做出示意图,直接写出![]() 与
与![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com