
【题目】如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.

【答案】(1)见解析;(2)10.
【解析】
(1)根据等边对等角可得∠ABC=∠ACB,根据三角形内角和定理可得∠MBP=∠HCP,然后可得∠PBC=∠PCB,可证PB=PC;
(2)利用AAS可直接证明△PMB≌△PHC,得到PM=PH=3,BM=CH,然后求出BM,在直角△ABH中利用勾股定理构建方程求出AM即可解决问题.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠PMB=∠PHC=90°,∠MPB=∠HPC,
∴∠MBP=∠HCP,
∴∠ABC-∠MBP =∠ACB-∠HCP,即∠PBC=∠PCB,
∴PB=PC;
(2)在△PMB和△PHC中,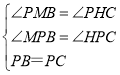 ,
,
∴△PMB≌△PHC(AAS),
∴PM=PH=3,BM=CH,
∴BM=![]() ,AM=AH,
,AM=AH,
在Rt△ABH中,AB2=AH2+BH2,
∴(4+AM)2= AH2+(5+3)2,即(4+AM)2= AM2+82,
解得:AM=6,
∴AB=AM+BM=6+4=10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB丄CD于点E,且AB = CD = AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC= 135°;②BD = BI,③S△AIC = S△BID ;④IF⊥AC.其中正确的是_________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为2的等边三角形ABC中,D点在边BC上运动(不与B、C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF.
(1)若∠AED=30°,则∠ADB=_______°.
(2)求证:△BED≌△CDF
(3)点D在BC边上从B至C的运动过程中,△BED周长变化规律为( )
A.不变 B.一直变小 C.先变大后变小 D.先变小后变大

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“频率具有稳定性”的试验时,绘出某一结果出现的频率折线图如图所示,则符合这一结果的试验可能是( )

A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,掷出的点数是5
C.任意写一个整数,它能被2整除
D.从一个装有2个红球和1个白球的袋子中任取一球(这些球除颜色外完全相同),取到的是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 为等边三角形,
为等边三角形,![]()
![]() ,垂足为点
,垂足为点![]() .
.![]()
![]() ,垂足为
,垂足为![]() .
.

(1)求OF的长;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() 交
交![]() 于E,求OE的长.
于E,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
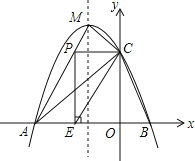
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点
与x轴交于A、B两点,与y轴交于点![]() ,且此抛物线的顶点坐标为
,且此抛物线的顶点坐标为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 设点D为已知抛物线对称轴上的任意一点,当
设点D为已知抛物线对称轴上的任意一点,当![]() 与
与![]() 面积相等时,求点D的坐标;
面积相等时,求点D的坐标;
![]() 点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将
点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将![]() 沿直线CE翻折,使点P的对应点
沿直线CE翻折,使点P的对应点![]() 与P、E、C处在同一平面内,请求出点
与P、E、C处在同一平面内,请求出点![]() 坐标,并判断点
坐标,并判断点![]() 是否在该抛物线上.
是否在该抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com