
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m﹣n)2=0,(n﹣4)2=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴n=4,m=4.
∴(m﹣n)2+(n﹣4)2=0,
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
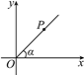
【题目】如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的夹角为α,则用[ρ,α]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[![]() ,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
A. (-2,2![]() ) B. (2,-2
) B. (2,-2![]() ) C. (-2
) C. (-2![]() ,-2) D. (-4,-4
,-2) D. (-4,-4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
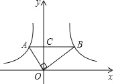
【题目】如图,在函数y1=![]() (x<0)和y2=
(x<0)和y2=![]() (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,则线段AB的长度=__.
,则线段AB的长度=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
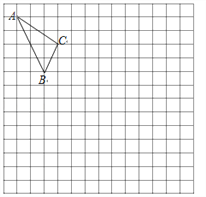
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com