
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,垂足分别是
,垂足分别是![]() 、
、![]() ,
,![]() .
.
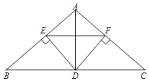
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求证:四边形
,求证:四边形![]() 是正方形.
是正方形.
【答案】证明见解析
【解析】
(1)根据相似三角形的性质得到![]() =
=![]() ,根据AB=AC,得到AE=AF,利用HL定理证明;
,根据AB=AC,得到AE=AF,利用HL定理证明;
(2)根据等腰三角形的性质得到BC=2BD,得到BD=AD,根据正方形的判定定理即可证明.
(1)∵△AEF∽△ABC,∴![]() =
=![]() .
.
∵AB=AC,∴AE=AF.
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.在Rt△AED和Rt△AFD中,∵![]() ,∴Rt△AED≌Rt△AFD;
,∴Rt△AED≌Rt△AFD;
(2)∵Rt△AED≌Rt△AFD,∴∠EAD=∠FAD.
∵AB=AC,∴AD⊥BC,BC=2BD.
∵BC=2AD,∴BD=AD.
∵AD⊥BC,∴∠ADB=90°,∴∠B=∠BAD=45°,∴∠BAC=2∠BAD=90°.
∵∠AED=∠AFD=90°,∴四边形AEDF是矩形.
∵AE=AF,∴矩形AEDF是正方形.


科目:初中数学 来源: 题型:
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
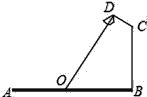
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
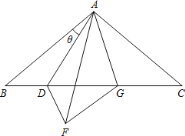
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索
小丽发现通过用两种不同的方法计算同一几何体体积,就可以得到一个恒等式.如图是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.

![]() ;
;
![]() ;
;
![]() 用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式为:________;
用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式为:________;
![]() 已知
已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的![]() 张卡片分成两组,每组
张卡片分成两组,每组![]() 张,分别标上
张,分别标上![]() 、
、![]() 、
、![]() ,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
![]() 请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
![]() 若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com