【题目】已知，如图，线段
长为
，
于
，
于
，
＝
，
＝
，
为线段上两动点，
在
右侧且＝
，则由
到
的路径：
的最小值为________．
【答案】
【解析】
过
作
且
＝
＝
，作
关于
的对称点″，连接″
交于点
，过作
交于
，由AA′//EF，AE//A′F可得四边形AEFA′是平行四边形，根据平行四边形的性质可得AE=A′F，根据轴对称的性质可得A′F=A″F，即可得出
的最小值＝″，进而可得
的值最小，过″作″
交
的延长线于
，利用勾股定理求出″的值即可求出的值.
过作且＝＝，作关于的对称点″，连接″交于点，过作交于，
∵AA′//EF，AE//A′F，
∴四边形AEFA′是平行四边形，
∴AE=A′F，
∵A′和A″关于CD对称，
∴A′F=A″F，
∴AE+FB=A″F+FB
∴的最小值＝″，此时，的值最小，的最小值＝″，
过″作″交的延长线于，
则″＝
，
＝
，
∴″＝
=
，
∴的最小值为，
科目：初中数学 来源： 题型：
【题目】如图，钝角△ABC中，AB=AC，BC=2
，O是边AB上一点，以O为圆心，OB为半径作⊙O，交边AB于点D，交边BC于点E，过E作⊙O的切线交边AC于点F．
（1）求证：EF⊥AC．
（2）连结DF，若∠ABC=30°，且DF∥BC，求⊙O的半径长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，直线AM⊥AN，AB平分∠MAN，过点B作BC⊥BA交AN于点C；动点E、D同时从A点出发，其中动点E以2cm/s的速度沿射线AN方向运动，动点D以1cm/s的速度运动；已知AC＝6cm，设动点D，E的运动时间为t．
（1）当点D在射线AM上运动时满足S△ADB：S△BEC＝2：1，试求点D，E的运动时间t的值；
（2）当动点D在直线AM上运动，E在射线AN运动过程中，是否存在某个时间t，使得△ADB与△BEC全等？若存在，请求出时间t的值；若不存在，请说出理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形ABCD中，点E是边CD的中点，将△ADE沿AE折叠得到△AFE，且点F在长方形ABCD内．将AF延长交边BC于点G．若BG=3CG，则
=（ ）
A.
B.1C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场购进甲、乙两种商品，甲种商品共用了
元，乙种商品共用了
元．已知乙种商品每件进价比甲种商品每件进价多
元，且购进的甲、乙两种商品件数相同．
求甲、乙两种商品的每件进价；
该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为
元，乙种商品的销售单价为
元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的九折销售；乙种商品销售单价保持不变．要使两种商品全部售完后共获利不少于
元，问甲种商品按原销售单价至少销售多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AB∥CD，过点D作DF⊥BC，垂足为F，DF与AC交于点M，已知∠1=∠2.
(1)求证：CM=DM；
(2)若FB=FC,求证：AM-MD=2FM.
查看答案和解析>>
科目：初中数学 来源： 题型：
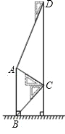
【题目】如图，某中学在教学楼前新建了一座雕塑
．为了测量雕塑的高度，小明在二楼找到一点
，利用三角尺测得雕塑顶端点
的仰角为
，底部点
的俯角为
，小华在五楼找到一点
，利用三角尺测得点的俯角为
．若
为
，则雕塑的高度为________
．（结果精确到
，参考数据：
）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴正方向的夹角为α，则用[ρ，α]表示点P的极坐标，例如：点P的坐标为(1，1)，则其极坐标为[
，45°]．若点Q的极坐标为[4，120°]，则点Q的坐标为( )
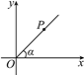
A. (－2，2
) B. (2，－2) C. (－2，－2) D. (－4，－4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
