
【题目】如图,长方形ABCD中,点E是边CD的中点,将△ADE沿AE折叠得到△AFE,且点F在长方形ABCD内.将AF延长交边BC于点G.若BG=3CG,则![]() =( )
=( )

A.![]() B.1C.
B.1C.![]() D.
D.![]()
【答案】B
【解析】
根据中点定义得出DE=CE,再根据折叠的性质得出DE=EF,AF=AD,∠AFE=∠D=90°,从而得出CE=EF,连接EG,利用“HL”证明△ECG≌△EFG,根据全等三角形性质得出CG=FG,设CG=![]() ,则BC=4
,则BC=4![]() ,根据长方形性质得出AD=BC=4
,根据长方形性质得出AD=BC=4![]() ,再求出AF=4
,再求出AF=4![]() ,最后求出AG=AF+FG=5
,最后求出AG=AF+FG=5![]() ,最后利用勾股定理求出AB,从而进一步得出答案即可.
,最后利用勾股定理求出AB,从而进一步得出答案即可.

如图,连接EG,
∵点E是CD中点,
∴DE=EC,
根据折叠性质可得:AD=AF,DE=EF,∠D=∠AFE=90°,
∴CE=EF,
在Rt△ECG与Rt△EFG中,
∵EG=EG,EC=EF,
∴Rt△ECG≌Rt△EFG(HL),
∴CG=FG,
设CG=![]() ,
,
∴BG=3CG=3![]() ,
,
∴BC=4![]() ,
,
∴AF=AD=BC=4![]() .
.
∴AG=5![]() .
.
在Rt△ABG中,
∴![]() ,
,
∴![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
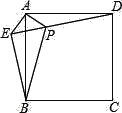
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时,某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.

(1)请计算最喜欢B项目的人数所占的百分比.
(2)请计算D项所在扇形图中的圆心角的度数.
(3)请把统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com