
【题目】如图,直线y=x+m与双曲线y=![]() 相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为_____.
相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为_____.
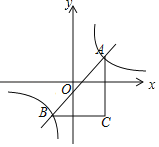
【答案】6
【解析】
根据双曲线y=![]() 过A,B两点,可设A(a,
过A,B两点,可设A(a,![]() ),B(b,
),B(b,![]() ),则C(a,
),则C(a,![]() ).将y=x+m代入y=
).将y=x+m代入y=![]() ,整理得x2+mx-3=0,由于直线y=x+m与双曲线y=
,整理得x2+mx-3=0,由于直线y=x+m与双曲线y=![]() 相交于A,B两点,所以a、b是方程x2+mx-3=0的两个根,根据根与系数的关系得出a+b=-m,ab=-3,那么(a-b)2=(a+b)2-4ab=m2+12.再根据三角形的面积公式得出S△ABC=
相交于A,B两点,所以a、b是方程x2+mx-3=0的两个根,根据根与系数的关系得出a+b=-m,ab=-3,那么(a-b)2=(a+b)2-4ab=m2+12.再根据三角形的面积公式得出S△ABC=![]() ACBC=
ACBC=![]() m2+6,利用二次函数的性质即可求出当m=0时,△ABC的面积有最小值6.
m2+6,利用二次函数的性质即可求出当m=0时,△ABC的面积有最小值6.
设A(a,![]() ),B(b,
),B(b,![]() ),则C(a,
),则C(a,![]() ).
).
将y=x+m代入y=![]() ,得x+m=
,得x+m=![]() ,
,
整理,得x2+mx-3=0,
则a+b=-m,ab=-3,
∴(a-b)2=(a+b)2-4ab=m2+12.
∵S△ABC=![]() ACBC
ACBC
=![]() (
(![]() -
-![]() )(a-b)
)(a-b)
=![]()
![]() (a-b)
(a-b)
=![]() (a-b)2
(a-b)2
=![]() (m2+12)
(m2+12)
=![]() m2+6,
m2+6,
∴当m=0时,△ABC的面积有最小值6.
故答案为6.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
A.0B.1C.2D.大于2的整数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
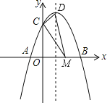
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() 点坐标为
点坐标为![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
![]() 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;
![]() 为
为![]() 轴上的一点,当
轴上的一点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节前夕,某超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点连线等方法,猜测并求出y与x之间的函数解析式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.

(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,点E是边CD的中点,将△ADE沿AE折叠得到△AFE,且点F在长方形ABCD内.将AF延长交边BC于点G.若BG=3CG,则![]() =( )
=( )

A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
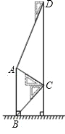
【题目】如图,某中学在教学楼前新建了一座雕塑![]() .为了测量雕塑的高度,小明在二楼找到一点
.为了测量雕塑的高度,小明在二楼找到一点![]() ,利用三角尺测得雕塑顶端点
,利用三角尺测得雕塑顶端点![]() 的仰角为
的仰角为![]() ,底部点
,底部点![]() 的俯角为
的俯角为![]() ,小华在五楼找到一点
,小华在五楼找到一点![]() ,利用三角尺测得点
,利用三角尺测得点![]() 的俯角为
的俯角为![]() .若
.若![]() 为
为![]() ,则雕塑
,则雕塑![]() 的高度为________
的高度为________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com