
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

【答案】(1)见解析;(2)![]()
【解析】
(1)因为EF为圆0的切线,故由此想到连接OE,得到∠OEF=90°,再根据OB和OE的关系找出∠OEB=∠C,判断出OE平行于AC,即可以得出EF⊥AC.
(2)连接DE、DF,设圆的半径为r,利用直径所对的圆周角是直角,得出∠DEB为直角,再根据 EF⊥AC,OE⊥AB,角与角之间的关系可以求出∠EDF为直角,利用勾股定理求出BE、EC的长,再根据BE+EC=![]() 可以求出圆O的半径.
可以求出圆O的半径.
(1)证明:连接OE,如图,
∵OB=OE,
∴∠B=∠OEB,
∵AB=AC,
∴∠B=∠C,
∴∠OEB=∠C,
∴OE∥AC,
∵EF为切线,
∴OE⊥EF,
∴EF⊥AC;
(2)解:连接DE,如图,设⊙O的半径长为r,
∵BD为直径,
∴∠BED=90°,
在Rt△BDE中,∵∠B=30°,
∴DE=![]() BD=r,BE=
BD=r,BE=![]() r,
r,
∵DF∥BC,
∴∠EDF=∠BED=90°,
∵∠C=∠B=30°,
∴∠CEF=60°,
∴∠DFE=∠CEF=60°,
在Rt△DEF中,DF=![]() r,
r,
∴EF=2DF=![]() r,
r,
在Rt△CEF中,CE=2EF=![]() r,
r,
而BC=2![]() ,
,
∴![]() r+
r+![]() r=2
r=2![]() ,解得r=
,解得r=![]() ,
,
即⊙O的半径长为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
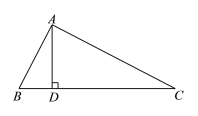
(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的高,AD的垂直平分线分别交AB,AC于点E,F.

(1)求证:∠B=![]() ∠AED;
∠AED;
(2)若添加条件:DE=DF.求证:∠B=∠C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
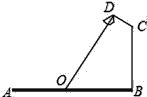
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每月可卖出
元,每月可卖出![]() 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨![]() 元每月要少卖
元每月要少卖![]() 件;售价每下降
件;售价每下降![]() 元每月要多卖
元每月要多卖![]() 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润;
![]() 为了使每月利润不少于
为了使每月利润不少于![]() 元应如何控制销售价格?
元应如何控制销售价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,形如![]() 的点涂上红色(其中
的点涂上红色(其中![]() 、
、![]() 为整数),称为红点,其余不涂色,那么抛物线
为整数),称为红点,其余不涂色,那么抛物线![]() 上有( )个红点.
上有( )个红点.
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D. 无数个
个 D. 无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com