
【题目】在平面直角坐标系中,形如![]() 的点涂上红色(其中
的点涂上红色(其中![]() 、
、![]() 为整数),称为红点,其余不涂色,那么抛物线
为整数),称为红点,其余不涂色,那么抛物线![]() 上有( )个红点.
上有( )个红点.
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D. 无数个
个 D. 无数个
【答案】B
【解析】
根据二次函数图象上的点的坐标特征知,形如(m,n2)的点(其中m、n为整数)均满足抛物线方程y=x2﹣2x+9,所以有n2=m2﹣2m+9,故可得出n2=(m﹣1)2+8,又因为m、n为整数,据此求m、n的值.
∵设点(m,n2)是抛物线y=x2﹣2x+9上的一个标准点,则n2=m2﹣2m+9,即n2﹣(m﹣1)2=8,∴(n﹣m+1)(n+m﹣1)=8.
∵m、n为整数,且n﹣m与n+m的奇偶性相同,∴n﹣m+1=2,n+m﹣1=4或n﹣m+1=4,n+m﹣1=2或n﹣m+1=﹣2,n+m﹣1=﹣4或n﹣m+1=﹣4,n+m﹣1=﹣2,∴抛物线y=x2﹣2x+9上有4个红点.
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
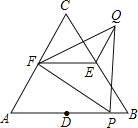
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是边长
分别是边长![]() 为的等边
为的等边![]() 的边
的边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() ,点
,点![]() 从顶点
从顶点![]() 同时出发,分别沿
同时出发,分别沿![]() ,
,![]() 边运动,点
边运动,点![]() 到点
到点![]() 停止,点
停止,点![]() 到点
到点![]() 停止.社运动时间为
停止.社运动时间为![]() 秒,他们的速度都为
秒,他们的速度都为![]() .
.

(1)连接![]() ,
,![]() 相交于
相交于![]() ,在点
,在点![]() ,
,![]() 的运动过程中
的运动过程中![]() 的大小是否变化?若变化,说明理由;若不变,求出它的度数;
的大小是否变化?若变化,说明理由;若不变,求出它的度数;
(2)当![]() 取何值时,
取何值时,![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 1 的正方形组成的网格中,△ ABC的顶点均在格点上,A(3,2), B(4, 3), C(1, 1)

(1)画出△ABC关于y轴对称的图形△ A′B′C′
(2)写出A′、B′、C′的坐标(直接写出答案) A′ ;B′ ;C′ ;
(3)写出△ A′B′C′的面积为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
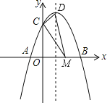
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() 点坐标为
点坐标为![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
![]() 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;
![]() 为
为![]() 轴上的一点,当
轴上的一点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节前夕,某超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点连线等方法,猜测并求出y与x之间的函数解析式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.

(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com