
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

【答案】(1)A(1,﹣4);
(2)△ABD是直角三角形,理由见解析;
(3)存在点P(﹣2,﹣7)或P(4,﹣1),使以点A、B、D、P为顶点的四边形是平行四边形.
【解析】试题分析:(1)先根据抛物线的解析式得出其对称轴方程,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标.
(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.
(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.
(1)∵顶点A的横坐标为![]() ,且顶点在y=x﹣5上,
,且顶点在y=x﹣5上,
∴当x=1时,y=1-5=-4,
∴A(1,-4).
(2)将A(1,-4)代入y=x2-2x+c,可得,1-2+c=-4,c=-3,
∴y=x2-2x-3,
∴B(0,-3)
当y=0时,x2-2x-3=0,x1=-1,x2=3
∴C(-1,0),D(3,0),
∵BD2=OB2+OD2=18,AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
∴BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)由题意知:直线y=x-5交y轴于点E(0,-5),交x轴于点F(5,0)
∴OE=OF=5,
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图,
过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.

设P(x1,x1-5),则G(1,x1-5)
则PG=|1-x1|,AG=|5-x1-4|=|1-x1|
PA=BD=3![]()
由勾股定理得:
(1-x1)2+(1-x1)2=18,x12-2x1-8=0,x1=-2或4
∴P(-2,-7)或P(4,-1),
存在点P(-2,-7)或P(4,-1)使以点A、B、D、P为顶点的四边形是平行四边形.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为( )

A.80°B.70°C.60°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子![]() 米跑项目,该校预先对这两名选手测试了
米跑项目,该校预先对这两名选手测试了![]() 次,测试成绩如下表
次,测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩(秒) |
|
|
|
|
|
|
|
|
乙的成绩(秒) |
|
|
|
|
|
|
|
|
![]() 为了衡量这两名选手
为了衡量这两名选手![]() 米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
![]() 你认为选派谁比较合适?为什么?
你认为选派谁比较合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011?菏泽)如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
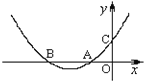
A. a+b=﹣1 B. a﹣b=﹣1
C. b<2a D. ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com