【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子
米跑项目，该校预先对这两名选手测试了
次，测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩（秒） |
|
|
|
|
|
|
|
|
乙的成绩（秒） |
|
|
|
|
|
|
|
|
为了衡量这两名选手米跑的水平，你选择哪些统计量？请分别求出这些统计量的值．
你认为选派谁比较合适？为什么？
科目：初中数学 来源： 题型：
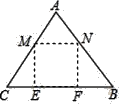
【题目】如图，王爷爷家院子里有一块三角形田地ABC，AB=AC=5米，BC=6米，现打算把它开垦出一个矩形MNFE区域种植韭菜，△AMN区域种植芹菜，△CME和△BNF区域种植青菜（开垦土地面积损耗均忽略不计），其中点M，N分别在AC，AB上，点E，F在BC上，已知韭菜每平方米收益100元，芹菜每平方米收益60元，青菜每平方米收益40元，设CM=5x米，王爷爷的蔬菜总收益为W元．
（1）当矩形MNFE恰好为正方形时，求韭菜种植区域矩形MNFE的面积．
（2）若种植韭菜的收益等于另两种蔬菜收益之和的2倍，求这时x的值．
（3）求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）请画出△ABC关于y轴对称的△DEF（其中D，E，F分别是A，B，C的对应点，不写画法）；
（2）直接写出D，E，F三点的坐标：D（ ），E（ ），F（ ）；
（3）在y轴上存在一点，使PC﹣PB最大，则点P的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=x2
2x+c的顶点A在直线l：y=x
5上．
（1）求抛物线顶点A的坐标；
（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；
（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点P(3m－6，m＋1)，试分别根据下列条件，求出点P的坐标．
(1)点P的横坐标比纵坐标大1；
(2)点P在过点A(3，－2)，且与x轴平行的直线上；
(3)点P到y轴的距离是到x轴距离的2倍．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】发现与探索
小丽发现通过用两种不同的方法计算同一几何体体积，就可以得到一个恒等式.如图是边长为
的正方体，被如图所示的分割线分成
块.
；
；
用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式为：________；
已知
，
，利用上面的规律求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在锐角△ABC中，AC＝8，△ABC的面积为20，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM＋MN的最小值是________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
如图，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA．下列四个判断中，不正确的是（ ）
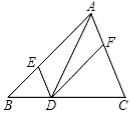
A．四边形AEDF是平行四边形
B．如果∠BAC=90°，那么四边形AEDF是矩形
C．如果AD平分∠BAC，那么四边形AEDF是矩形
D．如果AD⊥BC且AB=AC，那么四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
