
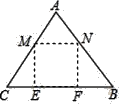
ΓΨΧβΡΩΓΩ»γΆΦΘ§Άθ“·“·Φ“‘ΚΉ”άο”–“ΜΩι»ΐΫ«–ΈΧοΒΊABCΘ§AB=AC=5ΟΉΘ§BC=6ΟΉΘ§œ÷¥ρΥψΑ―ΥϋΩΣΩ―≥ω“ΜΗωΨΊ–ΈMNFE«χ”ρ÷÷÷≤Ψ¬≤ΥΘ§ΓςAMN«χ”ρ÷÷÷≤«έ≤ΥΘ§ΓςCMEΚΆΓςBNF«χ”ρ÷÷÷≤«ύ≤ΥΘ®ΩΣΩ―ΆΝΒΊΟφΜΐΥπΚΡΨυΚω¬‘≤ΜΦΤΘ©Θ§Τδ÷–ΒψMΘ§NΖ÷±π‘ΎACΘ§AB…œΘ§ΒψEΘ§F‘ΎBC…œΘ§“―÷ΣΨ¬≤ΥΟΩΤΫΖΫΟΉ ’“φ100‘ΣΘ§«έ≤ΥΟΩΤΫΖΫΟΉ ’“φ60‘ΣΘ§«ύ≤ΥΟΩΤΫΖΫΟΉ ’“φ40‘ΣΘ§…ηCM=5xΟΉΘ§Άθ“·“·ΒΡ Ώ≤ΥΉή ’“φΈΣW‘ΣΘ°
Θ®1Θ©Β±ΨΊ–ΈMNFE«ΓΚΟΈΣ’ΐΖΫ–Έ ±Θ§«σΨ¬≤Υ÷÷÷≤«χ”ρΨΊ–ΈMNFEΒΡΟφΜΐΘ°
Θ®2Θ©»τ÷÷÷≤Ψ¬≤ΥΒΡ ’“φΒ»”ΎΝμΝΫ÷÷ Ώ≤Υ ’“φ÷°ΚΆΒΡ2±ΕΘ§«σ’β ±xΒΡ÷ΒΘ°
Θ®3Θ©«σΆθ“·“·ΒΡ Ώ≤ΥΉή ’“φΈΣWΙΊ”ΎxΒΡΚ· ΐ±μ¥ο ΫΦΑWΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©x=
ΘΜΘ®2Θ©x=![]() Μρ
Μρ![]() ;(3)W=©¹1200Θ®x©¹
;(3)W=©¹1200Θ®x©¹![]() Θ©2+912Θ§x=
Θ©2+912Θ§x=![]() ±Θ§W”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ912‘Σ
±Θ§W”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ912‘Σ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί≥…±»άΐΘ§…η“ΜΗωΈ¥÷Σ ΐΘ§Ά®ΙΐΙ¥Ι…Ε®άμ«σΫβ.Θ®2Θ©”Ο¥ζ ΐ Ϋ±μ ΨΗς÷÷ Ώ≤ΥΒΡ ’“φΘ§ΗυΨίΧθΦΰ–Έ≥…Β» ΫΘ§¥”Εχ«σΫβΘ§ΒΟ≥ωx.Θ®3Θ©”Οx±μ Ψ≥ωΗςΗω Ώ≤ΥΒΡ ’“φΘ§«σΚΆΈΣWΘ§¥”ΕχΉω≥ωΚ· ΐ ΫΘ§”ΟΕΰ¥ΈΚ· ΐΙφ¬…«σ≥ωΉν¥σ÷Β.
Θ®1Θ©ΉςAHΓΆBC”ΎHΘ§ΫΜMN”ΎDΘ°
ÿAB=ACȧAHâBCȧ
ΓύCH=HB=3Θ§
‘ΎRtΓςACH÷–Θ§AH=![]() =4Θ§
=4Θ§
ÿMEøAHȧ
Γύ![]() =
=![]() =
=![]() Θ§
Θ§
ΓύCE=3xΘ§EM=EF=4xΘ§
“Ή÷ΛΓςMECΓ’ΓςNFBΘ§
ΓύCE=BF=3xΘ§
Γύ3x+4x+3x=6Θ§
Γύx=![]() Θ§
Θ§
ΓύEM=![]() Θ§
Θ§
ΓύΨΊ–ΈMNFEΒΡΟφΜΐΈΣ![]() ΤΫΖΫΟΉΘ°
ΤΫΖΫΟΉΘ°
Θ®2Θ©”…Χβ“βΘΚ100ΓΝ4xΘ®6©¹6xΘ©=2[60ΓΝ![]() ΓΝΘ®6©¹6xΘ©Θ®4©¹4xΘ©+40ΓΝ4xΓΝ3x]Θ§
ΓΝΘ®6©¹6xΘ©Θ®4©¹4xΘ©+40ΓΝ4xΓΝ3x]Θ§
ΫβΒΟx=![]() Μρ
Μρ![]() Θ°
Θ°
Θ®3Θ©”…Χβ“βW=100ΓΝ4xΘ®6©¹6xΘ©+60ΓΝ![]() ΓΝΘ®6©¹6xΘ©Θ®4©¹4xΘ©+40ΓΝ4xΓΝ3x=©¹1200x2+960x+720=©¹1200Θ®x©¹
ΓΝΘ®6©¹6xΘ©Θ®4©¹4xΘ©+40ΓΝ4xΓΝ3x=©¹1200x2+960x+720=©¹1200Θ®x©¹![]() Θ©2+912Θ§
Θ©2+912Θ§
Θ§ΓΏ©¹1200ΘΦ0Θ§
Γύx=![]() ±Θ§W”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ912‘ΣΘ°
±Θ§W”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ912‘ΣΘ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏy=![]() x+4
x+4![]() Ζ÷±πΫΜx÷αΓΔy÷α”ΎΒψAΓΔCΘ§÷±œΏBC”κ÷±œΏACΙΊ”Ύy÷αΕ‘≥ΤΘ§Ε·ΒψD¥”ΒψA≥ωΖΔΘ§―ΊAC“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψC‘ΥΕ·Θ§Β±ΒψD≥ωΖΔΚσΘ§ΙΐΒψDΉςDEΓΈBCΫΜ’έœΏA©¹O©¹C”ΎΒψEΘ§“‘DEΈΣ±ΏΉςΒ»±ΏΓςDEFΘ§…ηΓςDEF”κΓςACO÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΒΡΟφΜΐΈΣSΘ§ΒψD‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°
Ζ÷±πΫΜx÷αΓΔy÷α”ΎΒψAΓΔCΘ§÷±œΏBC”κ÷±œΏACΙΊ”Ύy÷αΕ‘≥ΤΘ§Ε·ΒψD¥”ΒψA≥ωΖΔΘ§―ΊAC“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψC‘ΥΕ·Θ§Β±ΒψD≥ωΖΔΚσΘ§ΙΐΒψDΉςDEΓΈBCΫΜ’έœΏA©¹O©¹C”ΎΒψEΘ§“‘DEΈΣ±ΏΉςΒ»±ΏΓςDEFΘ§…ηΓςDEF”κΓςACO÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΒΡΟφΜΐΈΣSΘ§ΒψD‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°
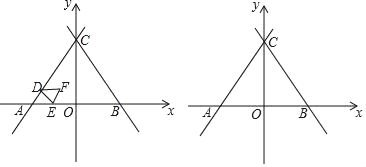
Θ®1Θ©–¥≥ωΉχ±ξΘΚΒψAΘ® ΓΓΘ©Θ§ΒψBΘ®ΓΓ ΓΓΘ©Θ§ΒψCΘ®ΓΓ ΓΓΘ©ΘΜ
Θ®2Θ©Β±ΒψE‘ΎœΏΕΈAO…œ ±Θ§«σS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©«σ≥ω“‘ΒψBΓΔEΓΔFΈΣΕΞΒψΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–Έ ±tΒΡ÷ΒΘΜ
Θ®4Θ©÷±Ϋ”–¥≥ωΒψF‘ΥΕ·ΒΡ¬Ζ≥Χ≥ΛΈΣΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
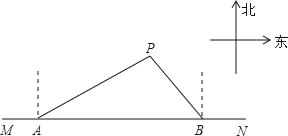
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΕΪΈςΖΫœρΒΡΚΘΑΕœΏMN…œ”–AΘ§BΝΫΥ“¥§Θ§¥§≥ΛΕΦ ’ΒΫ“―¥ΞΫΗΗι«≥ΒΡ¥§PΒΡ«σΨ»–≈Κ≈Θ§“―÷Σ¥§P‘Ύ¥§AΒΡ±±ΤΪΕΪ60ΓψΖΫœρ36ΚΘάο¥ΠΘ§¥§P‘Ύ¥§BΕΞΒψ±±ΤΪΈς37ΓψΖΫœρΘ§»τ¥§AΘ§¥§BΖ÷±π“‘30ΚΘάο/–Γ ±Θ§20ΚΘάο/–Γ ±ΒΡΥΌΕ»Ά§ ±≥ωΖΔΘ§‘»ΥΌ«ΑΆυΨ»‘°Θ§Ά®ΙΐΦΤΥψ≈–ΕœΡΡΥ“¥§œ»Βۥ不P¥ΠΘ°Θ®≤ΈΩΦ ΐΨί![]() =1.73Θ§sin37Γψ=0.6Θ§cos37Γψ=0.80Θ©
=1.73Θ§sin37Γψ=0.6Θ§cos37Γψ=0.80Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐ![]()
![]() «σ≥ω≈ΉΈοœΏ
«σ≥ω≈ΉΈοœΏ![]() ΒΡΕ‘≥Τ÷αΚΆΕΞΒψΉχ±ξΘΜ
ΒΡΕ‘≥Τ÷αΚΆΕΞΒψΉχ±ξΘΜ
![]() ‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±Ϋ”Μ≠≥ω≈ΉΈοœΏ
‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±Ϋ”Μ≠≥ω≈ΉΈοœΏ![]() Θ®ΉΔ“βΘΚΙΊΦϋΒψ“ΣΉΦ»ΖΘ§≤Μ±Ί–¥≥ωΜ≠ΆΦœσΒΡΙΐ≥ΧΘ©ΘΜ
Θ®ΉΔ“βΘΚΙΊΦϋΒψ“ΣΉΦ»ΖΘ§≤Μ±Ί–¥≥ωΜ≠ΆΦœσΒΡΙΐ≥ΧΘ©ΘΜ
![]() ΗυΨίΆΦœσΜΊ¥πΘΚ
ΗυΨίΆΦœσΜΊ¥πΘΚ
ΔΌ![]() »Γ ≤Ο¥÷Β ±Θ§≈ΉΈοœΏ‘Ύ
»Γ ≤Ο¥÷Β ±Θ§≈ΉΈοœΏ‘Ύ![]() ÷αΒΡ…œΖΫΘΩ
÷αΒΡ…œΖΫΘΩ
ΔΎ![]() »Γ ≤Ο¥÷Β ±Θ§
»Γ ≤Ο¥÷Β ±Θ§![]() ΒΡ÷ΒΥφ
ΒΡ÷ΒΥφ![]() ΒΡ÷ΒΒΡ‘ω¥σΕχΦθ–ΓΘΩ
ΒΡ÷ΒΒΡ‘ω¥σΕχΦθ–ΓΘΩ
![]() ΗυΨίΆΦœσ÷±Ϋ”–¥≥ω≤ΜΒ» Ϋ
ΗυΨίΆΦœσ÷±Ϋ”–¥≥ω≤ΜΒ» Ϋ![]() ΒΡΫβΦ·Θ°
ΒΡΫβΦ·Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
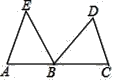
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABE÷–Θ§CΈΣ±ΏAB―”≥ΛœΏ…œ“ΜΒψΘ§BC=AEΘ§ΒψD‘ΎΓœEBCΡΎ≤ΩΘ§«“ΓœEBD=ΓœA=ΓœDCBΘ°
Θ®1Θ©«σ÷ΛΘΚΓςABEΓ’ΓςCDBΘ°
Θ®2Θ©Ν§ΫαDEΘ§»τΓœCDB=60ΓψΘ§ΓœAEB=50ΓψΘ§«σΓœBDEΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ 1 ΒΡ’ΐΖΫ–ΈΉι≥…ΒΡΆχΗώ÷–Θ§Γς ABCΒΡΕΞΒψΨυ‘ΎΗώΒψ…œΘ§A(3Θ§2), B(4Θ§ 3), C(1Θ§ 1)

(1)Μ≠≥ωΓςABCΙΊ”Ύy÷αΕ‘≥ΤΒΡΆΦ–ΈΓς AΓδBΓδCΓδ
(2)–¥≥ωAΓδΓΔBΓδΓΔCΓδΒΡΉχ±ξ(÷±Ϋ”–¥≥ω¥πΑΗ) AΓδ ;BΓδ ;CΓδ ;
(3)–¥≥ωΓς AΓδBΓδCΓδΒΡΟφΜΐΈΣ .(÷±Ϋ”–¥≥ω¥πΑΗ)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
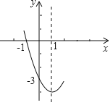
ΓΨΧβΡΩΓΩ“―÷ΣΘ§≈ΉΈοœΏ![]() ΒΡ≤ΩΖ÷ΆΦœσ»γΆΦΘ§‘ρœ¬Ν–ΥΒΖ®ΘΚΔΌΕ‘≥Τ÷α «÷±œΏ
ΒΡ≤ΩΖ÷ΆΦœσ»γΆΦΘ§‘ρœ¬Ν–ΥΒΖ®ΘΚΔΌΕ‘≥Τ÷α «÷±œΏ![]() ΘΜΔΎΒ±
ΘΜΔΎΒ±![]() ±Θ§
±Θ§![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔήΖΫ≥Χ
ΘΜΔήΖΫ≥Χ![]() Έό Β ΐΗυΘ§Τδ÷–’ΐ»ΖΒΡ”–________Θ°
Έό Β ΐΗυΘ§Τδ÷–’ΐ»ΖΒΡ”–________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§AB=10Θ§AC=8Θ°œΏΕΈAD”…œΏΕΈAB»ΤΒψAΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ90ΓψΒΟΒΫΘ§ΓςEFG”…ΓςABC―ΊCBΖΫœρΤΫ“ΤΒΟΒΫΘ§«“÷±œΏEFΙΐΒψDΘ°
Θ®1Θ©«σΓœBDFΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σCGΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ¥”ΝΫΟϊ”≈–ψ―Γ ÷÷–―Γ“ΜΟϊ≤ΈΦ”»Ϊ –÷––Γ―ß‘ΥΕ·ΜαΒΡΡ–Ή”![]() ΟΉ≈ήœνΡΩΘ§ΗΟ–Θ‘Λœ»Ε‘’βΝΫΟϊ―Γ ÷≤β ‘ΝΥ
ΟΉ≈ήœνΡΩΘ§ΗΟ–Θ‘Λœ»Ε‘’βΝΫΟϊ―Γ ÷≤β ‘ΝΥ![]() ¥ΈΘ§≤β ‘≥…Φ®»γœ¬±μ
¥ΈΘ§≤β ‘≥…Φ®»γœ¬±μ
|
|
|
|
|
|
|
| |
ΦΉΒΡ≥…Φ®Θ®ΟκΘ© |
|
|
|
|
|
|
|
|
““ΒΡ≥…Φ®Θ®ΟκΘ© |
|
|
|
|
|
|
|
|
![]() ΈΣΝΥΚβΝΩ’βΝΫΟϊ―Γ ÷
ΈΣΝΥΚβΝΩ’βΝΫΟϊ―Γ ÷![]() ΟΉ≈ήΒΡΥ°ΤΫΘ§Ρψ―Γ‘ώΡΡ–©Ά≥ΦΤΝΩΘΩ«κΖ÷±π«σ≥ω’β–©Ά≥ΦΤΝΩΒΡ÷ΒΘ°
ΟΉ≈ήΒΡΥ°ΤΫΘ§Ρψ―Γ‘ώΡΡ–©Ά≥ΦΤΝΩΘΩ«κΖ÷±π«σ≥ω’β–©Ά≥ΦΤΝΩΒΡ÷ΒΘ°
![]() Ρψ»œΈΣ―Γ≈…Υ≠±»ΫœΚœ ΘΩΈΣ ≤Ο¥ΘΩ
Ρψ»œΈΣ―Γ≈…Υ≠±»ΫœΚœ ΘΩΈΣ ≤Ο¥ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com