
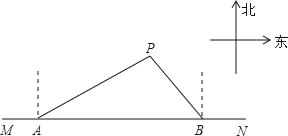
【题目】如图,在东西方向的海岸线MN上有A,B两艘船,船长都收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向36海里处,船P在船B顶点北偏西37°方向,若船A,船B分别以30海里/小时,20海里/小时的速度同时出发,匀速前往救援,通过计算判断哪艘船先到达船P处.(参考数据![]() =1.73,sin37°=0.6,cos37°=0.80)
=1.73,sin37°=0.6,cos37°=0.80)
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】某校在推进新课改的过程中,开设的“课程超市”有:A.炫彩剧社,B.烹饪,C.游泳,D.羽毛球,E.科技等五个科目,学生可根据自己的爱好选修一门,负责“课程超市”的老师对七年级一班全体同学的选课情况进行调查统计,并将结果绘制成了如下两幅尚不完整的统计图:
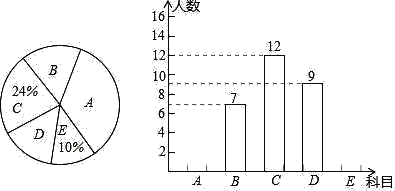
根据图中提供的信息,解答下列问题:
(1)请求出该班的总人数;
(2)扇形统计图中,D所在扇形的圆心角度数为 ,并补全条形统计图;
(3)该班班委4人中,1人选修炫彩剧社,2人选修烹饪,1人选修游泳,老师要从这4人中任选2人了解他们对“课程超市”课程安排的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修炫彩剧社,1人选修烹饪的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=10,BC=16,点F是边BC上不与点B,C重合的一个动点,直线DE垂直平分BF,垂足为D.当△ACF是直角三角形时,线段BD的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为Rt△ABC的斜边,∠CBA=30°,△ABD,△ACF,△BCE均为正三角形,四边形MNPE是长方形,点F在MN上,点D在NP上,若AC=2,则图中空白部分的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
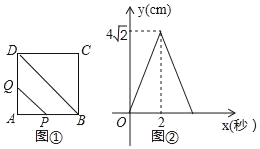
【题目】如图①,在边长为4cm的正方形ABCD中,点P以每秒2cm的速度从点A出发,沿AB→BC的路径运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动2.5秒时,PQ的长度是________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题
数学课上,老师出示了这样一道题:如图,![]() 中,
中,![]() ,点P为边AB上一点(不与A、B重合),过P作
,点P为边AB上一点(不与A、B重合),过P作![]() 于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段
于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段![]() 之间的数量关系并证明.
之间的数量关系并证明.
同学们经过思考后,交流了自已的想法
小明:“通过观察和度量,发现![]() 为直角.”
为直角.”
小伟:“我通过一线三直角的模型构造三角形全等可以解决问题.”
小强:“我构造等腰直角三角形,再利用全等三角形可以解决问题.”
老师:“若其他条件不变,PE=![]() AC,就可以求出
AC,就可以求出![]() 的值.”
的值.”
(1)![]() 多少度?四边形
多少度?四边形![]() 为什么特殊四边形?(直接写出答案)
为什么特殊四边形?(直接写出答案)
(2)探究线段![]() 之间的数量关系并证明;
之间的数量关系并证明;
(3)若其他条件不变,PE=![]() AC,求
AC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
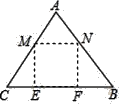
【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com