
ЁОЬтФПЁПФГаЃдкЭЦНјаТПЮИФЕФЙ§ГЬжаЃЌПЊЩшЕФЁАПЮГЬГЌЪаЁБгаЃКAЃЎьХВЪОчЩчЃЌBЃЎХытПЃЌCЃЎгЮгОЃЌDЃЎг№УЋЧђЃЌEЃЎПЦММЕШЮхИіПЦФПЃЌбЇЩњПЩИљОнздМКЕФАЎКУбЁаовЛУХЃЌИКд№ЁАПЮГЬГЌЪаЁБЕФРЯЪІЖдЦпФъМЖвЛАрШЋЬхЭЌбЇЕФбЁПЮЧщПіНјааЕїВщЭГМЦЃЌВЂНЋНсЙћЛцжЦГЩСЫШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃК
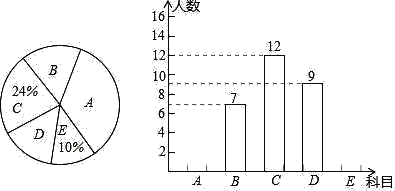
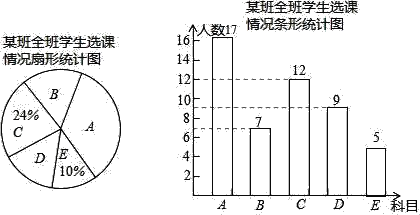
ИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыЧѓГіИУАрЕФзмШЫЪ§ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌDЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁ ЁЁЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУАрАрЮЏ4ШЫжаЃЌ1ШЫбЁаоьХВЪОчЩчЃЌ2ШЫбЁаоХытПЃЌ1ШЫбЁаогЮгОЃЌРЯЪІвЊДгет4ШЫжаШЮбЁ2ШЫСЫНтЫћУЧЖдЁАПЮГЬГЌЪаЁБПЮГЬАВХХЕФПДЗЈЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓбЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ50ЃЛЃЈ2ЃЉ64.8ЁуЃЌЭМЯъМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)гУCзщЕФШЫЪ§Г§вдЫќЫљеМЕФАйЗжБШМДПЩЕУЕНШЋАрШЫЪ§;
(2)гУDзщЕФЫљеМАйЗжБШГЫвд360ЁЃМДПЩЕУЕНдкЩШаЮЭГМЦЭМжа"DЁБЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЌЯШМЦЫуГіEзщШЫЪ§КЭAзщШЫЪ§ЃЌШЛКѓВЙШЋЦЕЪ§ЗжВМжБЗНЭМ;
(3)ЯШЛЪїзДЭМеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌевГібЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЫљеМНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНт.
ЃЈ1ЃЉИУАрЕФзмШЫЪ§ЮЊ12ЁТ24%=50ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊЃК50ЃЛ
ЃЈ2ЃЉБэЪОDЫљдкЩШаЮЕФдВаФНЧЪЧ360ЁуЁС![]() =64.8ЁуЃЌ
=64.8ЁуЃЌ
EПЦФПШЫЪ§ЮЊ50ЁС10%=5ЃЈШЫЃЉЃЌAПЦФПШЫЪ§ЮЊ50ЉЃЈ7+12+9+5ЃЉ=17ЃЈШЫЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
ЙЪД№АИЮЊЃК64.8ЁуЃЛ
ЃЈ3ЃЉЛЪїзДЭМЮЊЃК
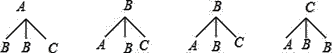
ЙВга12жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжабЁГіЕФ2ШЫжаЃЌ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФеМ4жжЃЌЫљвдбЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФИХТЪ=![]() =
=![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЙигк
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЕФНтЮЊ ЃЎ
ЕФНтЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() Еу
Еу![]() ДгЕу
ДгЕу![]() ПЊЪМби
ПЊЪМби![]() БпЯђ
БпЯђ![]() вд
вд![]() ЕФЫйЖШвЦЖЏЃЌЕу
ЕФЫйЖШвЦЖЏЃЌЕу![]() Дг
Дг![]() ЕуПЊЪМби
ЕуПЊЪМби![]() БпЯђЕу
БпЯђЕу![]() вд
вд![]() ЕФЫйЖШвЦЖЏЃЎШчЙћ
ЕФЫйЖШвЦЖЏЃЎШчЙћ![]() ЁЂ
ЁЂ![]() ЗжБ№Дг
ЗжБ№Дг![]() ЃЌ
ЃЌ![]() ЭЌЪБГіЗЂЃЌЯпЖЮ
ЭЌЪБГіЗЂЃЌЯпЖЮ![]() ФмЗёНЋ
ФмЗёНЋ![]() ЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃПШєФмЃЌЧѓГідЫЖЏЪБМфЃЛШєВЛФмЫЕУїРэгЩЃЎ
ЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃПШєФмЃЌЧѓГідЫЖЏЪБМфЃЛШєВЛФмЫЕУїРэгЩЃЎ
![]() Шє
Шє![]() ЕубиЩфЯп
ЕубиЩфЯп![]() ЗНЯђДг
ЗНЯђДг![]() ЕуГіЗЂвд
ЕуГіЗЂвд![]() ЕФЫйЖШвЦЖЏЃЌЕу
ЕФЫйЖШвЦЖЏЃЌЕу![]() биЩфЯп
биЩфЯп![]() ЗНЯђДг
ЗНЯђДг![]() ЕуГіЗЂвд
ЕуГіЗЂвд![]() ЕФЫйЖШвЦЖЏЃЌ
ЕФЫйЖШвЦЖЏЃЌ![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂЃЌЮЪМИУыКѓЃЌ
ЭЌЪБГіЗЂЃЌЮЪМИУыКѓЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃП
ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌИлПк![]() ЮЛгкИлПк
ЮЛгкИлПк![]() е§ЮїЗНЯђ
е§ЮїЗНЯђ![]() ДІЃЌаЁЕК
ДІЃЌаЁЕК![]() ЮЛгкИлПк
ЮЛгкИлПк![]() ББЦЋЮї
ББЦЋЮї![]() ЕФЗНЯђЃЎвЛЫвгЮДЌДгИлПк
ЕФЗНЯђЃЎвЛЫвгЮДЌДгИлПк![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЗНЯђЃЈББЦЋЮї
ЗНЯђЃЈББЦЋЮї![]() ЃЉвд
ЃЉвд![]() ЕФЫйЖШЪЛРыИлПк
ЕФЫйЖШЪЛРыИлПк![]() ЃЌЭЌЪБвЛЫвПьЭЇДгИлПк
ЃЌЭЌЪБвЛЫвПьЭЇДгИлПк![]() ГіЗЂЃЌбиББЦЋЖЋ
ГіЗЂЃЌбиББЦЋЖЋ![]() ЕФЗНЯђвд
ЕФЗНЯђвд![]() ЕФЫйЖШЪЛЯђаЁЕК
ЕФЫйЖШЪЛЯђаЁЕК![]() ЃЌдкаЁЕК
ЃЌдкаЁЕК![]() гУ
гУ![]() МгзАВЙИјЮязЪКѓЃЌСЂМДАДдРДЕФЫйЖШИјгЮДЌЫЭШЅЃЎ
МгзАВЙИјЮязЪКѓЃЌСЂМДАДдРДЕФЫйЖШИјгЮДЌЫЭШЅЃЎ
![]() ПьЭЇДгИлПк
ПьЭЇДгИлПк![]() ЕНаЁЕК
ЕНаЁЕК![]() ашвЊЖрГЄЪБМфЃП
ашвЊЖрГЄЪБМфЃП
![]() ШєПьЭЇДгаЁЕК
ШєПьЭЇДгаЁЕК![]() ЕНгыгЮДЌЯргіЧЁКУгУЪБ
ЕНгыгЮДЌЯргіЧЁКУгУЪБ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕМАЯргіДІгыИлПк
ЕФжЕМАЯргіДІгыИлПк![]() ЕФОрРыЃЎ
ЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
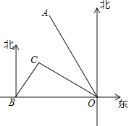
ЁОЬтФПЁПШчЭМЃЌдквЛПУЪїCDЕФ10mИпДІЕФBЕугаСНжЛКязгЃЌЫќУЧЖМвЊЕНAДІГиЬСБпКШЫЎЃЌЦфжавЛжЛКязгбиЪїХРЯТзпЕНРыЪї20mДІЕФГиЬСAДІЃЌСэвЛжЛКязгХРЕНЪїЖЅDКѓжБЯпдОШыГиЬСЕФAДІЃЎШчЙћСНжЛКязгЫљОЙ§ЕФТЗГЬЯрЕШЃЌЪдЮЪетПУЪїЖрИпЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаЙигкздШЛЪ§ЕФЕШЪНЃК
ЃЈ1ЃЉ32Љ4ЁС12=5 Ђй
ЃЈ2ЃЉ52Љ4ЁС22=9 Ђк
ЃЈ3ЃЉ72Љ4ЁС32=13 Ђл
Ё ИљОнЩЯЪіЙцТЩНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭъГЩЕкЮхИіЕШЪНЃК112Љ4ЁС ______2= ЃЛ
ЃЈ2ЃЉаДГіФуВТЯыЕФЕк n ИіЕШЪНЃЈгУКЌ n ЕФЪНзгБэЪОЃЉЃЌВЂбщжЄЦфе§ШЗадЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
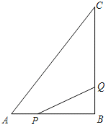
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌЕуAЁЂBЁЂCдкаЁе§ЗНаЮЕФЖЅЕуЩЯ.
(1)дкЭМжаЛГігыЁїABCЙигкжБЯпlГЩжсЖдГЦЕФЁїAЁфBЁфCЁф.
(2)ЫФБпаЮ ABCAЁфЕФУцЛ§ЮЊ_____ЃЛ
(3)дкжБЯпlЩЯеввЛЕуPЃЌЪЙPA+PBЕФГЄзюЖЬЃЌдђетИізюЖЬГЄЖШЮЊ______.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=![]() x+4
x+4![]() ЗжБ№НЛxжсЁЂyжсгкЕуAЁЂCЃЌжБЯпBCгыжБЯпACЙигкyжсЖдГЦЃЌЖЏЕуDДгЕуAГіЗЂЃЌбиACвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЕБЕуDГіЗЂКѓЃЌЙ§ЕуDзїDEЁЮBCНЛелЯпAЉOЉCгкЕуEЃЌвдDEЮЊБпзїЕШБпЁїDEFЃЌЩшЁїDEFгыЁїACOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуDдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЗжБ№НЛxжсЁЂyжсгкЕуAЁЂCЃЌжБЯпBCгыжБЯпACЙигкyжсЖдГЦЃЌЖЏЕуDДгЕуAГіЗЂЃЌбиACвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЌЕБЕуDГіЗЂКѓЃЌЙ§ЕуDзїDEЁЮBCНЛелЯпAЉOЉCгкЕуEЃЌвдDEЮЊБпзїЕШБпЁїDEFЃЌЩшЁїDEFгыЁїACOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуDдЫЖЏЕФЪБМфЮЊtУыЃЎ
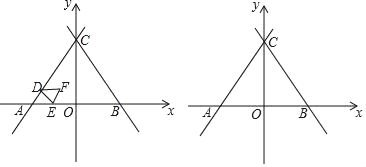
ЃЈ1ЃЉаДГізјБъЃКЕуAЃЈ ЁЁЃЉЃЌЕуBЃЈЁЁ ЁЁЃЉЃЌЕуCЃЈЁЁ ЁЁЃЉЃЛ
ЃЈ2ЃЉЕБЕуEдкЯпЖЮAOЩЯЪБЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЧѓГівдЕуBЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЪБtЕФжЕЃЛ
ЃЈ4ЃЉжБНгаДГіЕуFдЫЖЏЕФТЗГЬГЄЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
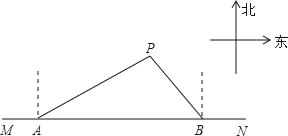
ЁОЬтФПЁПШчЭМЃЌдкЖЋЮїЗНЯђЕФКЃАЖЯпMNЩЯгаAЃЌBСНЫвДЌЃЌДЌГЄЖМЪеЕНвбДЅНИИщЧГЕФДЌPЕФЧѓОШаХКХЃЌвбжЊДЌPдкДЌAЕФББЦЋЖЋ60ЁуЗНЯђ36КЃРяДІЃЌДЌPдкДЌBЖЅЕуББЦЋЮї37ЁуЗНЯђЃЌШєДЌAЃЌДЌBЗжБ№вд30КЃРя/аЁЪБЃЌ20КЃРя/аЁЪБЕФЫйЖШЭЌЪБГіЗЂЃЌдШЫйЧАЭљОШдЎЃЌЭЈЙ§МЦЫуХаЖЯФФЫвДЌЯШЕНДяДЌPДІЃЎЃЈВЮПМЪ§Он![]() =1.73ЃЌsin37Ёу=0.6ЃЌcos37Ёу=0.80ЃЉ
=1.73ЃЌsin37Ёу=0.6ЃЌcos37Ёу=0.80ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com