
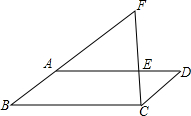
 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )| A. | 6cm2 | B. | 9cm2 | C. | 18cm2 | D. | 27cm2 |
分析 根据平行四边形的性质得BC=AD,BC∥AD,CD∥AB,∠D=∠B,则BC=3DE,再证明△CDE∽△FBC,然后利用三角形相似的性质可计算出△BCF的面积.
解答 解:∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,CD∥AB,∠D=∠B,
∵AE=2ED,
∴BC=3DE,
∵CD∥AF,
∴∠DCE=∠F,
∴△CDE∽△FBC,
∴$\frac{{S}_{△CDE}}{{S}_{△FBC}}$=($\frac{DE}{BC}$)2=$\frac{1}{9}$,
∴S△FBC=9×3=27(cm2).
故选D.
点评 本题考查了相似三角形的判定与性质:两个三角形相似对应角相等,对应边的比相等;相似三角形面积的比等于相似比的平方.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 4道 | B. | 3道 | C. | 2道 | D. | 1道 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
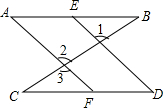 已知:如图,∠B=∠C,∠1=∠3.求证:∠A=∠D.
已知:如图,∠B=∠C,∠1=∠3.求证:∠A=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
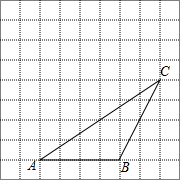 如图,△ABC的顶点都在边长为1的正方形方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
如图,△ABC的顶点都在边长为1的正方形方格纸的格点上.将△ABC向左平移2格,再向上平移4格.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
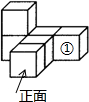 如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形( )
如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形( )| A. | 主视图改变,左视图改变 | B. | 俯视图不变,左视图不变 | ||
| C. | 俯视图改变,左视图改变 | D. | 主视图改变,左视图不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
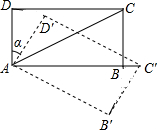 如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.
如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com