
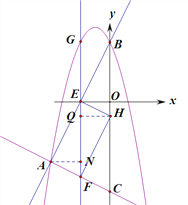
����Ŀ����ͼ��������y=-x2+bx+c��ֱ��AB����A(-4��-4)��B(0��4)���㣬ֱ��AC��y=-![]() x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
��1����������y=-x2+bx+c�ı���ʽ��
��2������GB��EO�����ı���GEOB��ƽ���ı���ʱ�����G�����ꣻ
��3������y���ϴ���һ��H������EH��HF������E�˶���ʲôλ��ʱ����A��E��F��HΪ������ı����Ǿ��Σ������ʱ��E��H�����ꣻ
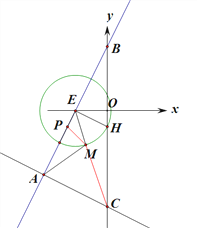
���ڢٵ�ǰ���£��Ե�EΪԲ�ģ�EH��Ϊ�뾶��Բ����MΪ��E��һ���㣬��![]() AM+CM����Сֵ.
AM+CM����Сֵ.

���𰸡���1��y=-x2-2x+4����2��G(-2��4)����3����H(0��-1)����![]()
����������������1�����ô���ϵ������������߽���ʽ��
��2�������ô���ϵ�������ֱ��AB�Ľ���ʽ����������ƽ���ı��εĶԱ���Ƚ���������⼴�ɣ�
��3�������жϳ�Ҫ�Ե�A��E��F��HΪ������ı����Ǿ��Σ�ֻ��EFΪ�Խ��ߣ������е����깫ʽ�������̼��ɣ�
����ȡEG���е�P�����жϳ���PEM�ס�MEA���ɵó�PM=![]() AM������CP��ԲE��M���������P�����꼴�ɵó����ۣ�
AM������CP��ԲE��M���������P�����꼴�ɵó����ۣ�
��⣺��1����1���ߵ�A��-4��-4����B��0��4����������y=-x2+bx+c�ϣ�
��![]() ��
��
��![]() ��
��
�������ߵĽ���ʽΪy=-x2-2x+4��
��2����ֱ��AB�ı���ʽΪy=kx+b
��ֱ��AB����A(-4��-4)��B(0��4)��
��![]() �����
�����![]() ��
��
��y=2x+4
��E(m��2m+4)����G(m��-m2-2m+4)
���ı���GEOB��ƽ���ı��Σ�
��GE=OB=4��
��-m2-2m+4-2m-4=4�����m=-2
��G(-2��4)
��3������E(m��2m+4)����F(m��-![]() m-6)
m-6)
��A��AN��EG����H��HQ��EG
�ı���AFHE�Ǿ��Σ����PFN�ա�HEQ����AN=QH����m+4=-m�����m=-2��E(-2��0)
EQ=FN=-4+![]() m+6=1
m+6=1
��H(0��-1)
��������ɵã�E(-2��0)��H(0��-1),��EH=![]() ������E�İ뾶Ϊ
������E�İ뾶Ϊ![]() ��
��
��M���ڡ�E�ϣ���EM=![]()
��A(-4��-4)��E(-2��0)����AE=2![]()
��AE�Ͻ�ȡEP=![]() EM����EP=
EM����EP=![]() ������PM��
������PM��
����EPM����EMA����![]() =
=![]() =
=![]() =
=![]() =
=![]() ����PEM=��MEA������EPM����EMA��PM=
����PEM=��MEA������EPM����EMA��PM=![]() AM
AM
���߶�PC�ij���Ϊ![]() AM+CM����Сֵ
AM+CM����Сֵ
��EP=![]() EM=
EM=![]() AE=
AE=![]() ��2
��2![]() =
=![]() ��AP=AE-PE=
��AP=AE-PE=![]() , AC=2
, AC=2![]() ��PC=
��PC=![]()
��![]() AM+CM����СֵΪ
AM+CM����СֵΪ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y1��kx+b��y2��x+a��ͼ����ͼ��ʾ�������н��ۣ���k��0����a��0������x��3ʱ��y1��y2������y1��0��y2��0ʱ����a��x��4��������ȷ�ĸ����ǣ�������

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
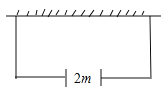
����Ŀ����ͼ����Ҫ��һ�������μ�����������һ�߿�ǽ��ǽ������һ��2�����ţ��������������Χ�ɣ�����ܳ�33�ף�Χ�ɳ����εļ�������֮�����ܲ����п�϶����
��1����ǽ��Ϊ18�ף�ҪΧ�ɼ��������Ϊ150ƽ���ף����ij��Ϳ���Ϊ�����ף�
��2��Χ�ɼ�����������ܴﵽ200ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�Rt��AOB������ֱ�DZ�OA��OB�ֱ���x���y���ϣ�OA=3��OB=4���ѡ�AOB�Ƶ�A˳ʱ����ת120�㣬�õ���ADC����OB�ϵ�һ��M��ת��Ķ�Ӧ��ΪM�䣬��AM��+DMȡ����Сֵʱ����M������Ϊ��������

A. ��0��![]() �� B. ��0��
�� B. ��0��![]() �� C. ��0��
�� C. ��0��![]() �� D. ��0��3��
�� D. ��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2�������ǰ�|x1��x2|+|y1��y2|����P1��P2������ֱ�Ǿ��룬����d��P1��P2����
��1����֪OΪ����ԭ�㣬����P��x��y������d��O��P��=1����д��x��y֮������Ĺ�ϵʽ������������ֱ������ϵ�л������з��������ĵ�P����ɵ�ͼ�Σ�
��2����P0��x0��y0����һ���㣬Q��x��y����ֱ��y=ax+b�ϵĶ��㣬���ǰ�d��P0��Q������Сֵ����P0��ֱ��y=ax+b��ֱ�Ǿ��룮�����M��2��1����ֱ��y=x+2��ֱ�Ǿ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC�У���BAC��90�㣬AD��BC�ڵ�D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬AM���ӳ��߽�BC�ڵ�N������DM�����н��ۣ���AE��AF����DF��DN����AN��BF����EN��NC����AE��NC��������ȷ���۵ĸ����ǣ�������

A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڵ�����ABC�У�AB=AC=![]() ��BC=4����D��A������ÿ��
��BC=4����D��A������ÿ��![]() ����λ���ٶ����B�˶���ͬʱ��E�ӵ�B������ÿ��4����λ���ٶ����C�˶�����DE���Ҳ�����DEF=��B����ֱ��AC�ڵ�F�����˶���ʱ��Ϊt�룬����ADF��һ����ADΪ���ĵ���������ʱ��t��ֵΪ_____��
����λ���ٶ����B�˶���ͬʱ��E�ӵ�B������ÿ��4����λ���ٶ����C�˶�����DE���Ҳ�����DEF=��B����ֱ��AC�ڵ�F�����˶���ʱ��Ϊt�룬����ADF��һ����ADΪ���ĵ���������ʱ��t��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C������ͬһֱ���ϣ��ֱ���AB��BCΪ�ߣ���ֱ��AC��ͬ�����ȱ���ABD�͵ȱ���BCE������AE��BD�ڵ�M������CD��BE�ڵ�N������MN����BMN��

��1����֤��AE��CD��
��2�����ж���BMN����״����˵�����ɣ�
��3����CD��AE�ཻ�ڵ�G�����AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���м��������ɹ�Աȥͬһ�����Ϲ�˾�ֱ����������ϣ����ι������ϼ۸�ֱ�ΪmԪ/ǧ�˺�nԪ/ǧ�ˣ���m��n�������ɹ�Ա�IJɹ���ʽҲ��ͬ�����м�ÿ�ι���1000ǧ�ˣ���ÿ����ȥ800Ԫ�������ܹ����������.
(1)�ס����������ϵ�ƽ�����۸��Ƕ��٣�(����ĸm��n��ʾ)
(2)˭�Ĺ�����ʽ�����㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com