
【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )

A. (0,![]() ) B. (0,
) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,3)
) D. (0,3)
【答案】A
【解析】
根据旋转的性质得到AM=AM′,得出AM′+DM的最小值=AM+DM的最小值,作点D关于直线OB的对称点D′,连接AD′交OB于M,则AD′=AM′+DM的最小值,过D作DE⊥x轴于E,解直角三角形得到DE=![]() ×3=
×3=![]() ,AE=
,AE=![]() ,求出D(
,求出D(![]() ,
,![]() ),根据轴对称的性质得到D′(
),根据轴对称的性质得到D′(![]() ,
,![]() ),求出直线AD′的解析式为y=
),求出直线AD′的解析式为y=![]() x+
x+![]() ,于是得到结论.
,于是得到结论.
∵把△AOB绕点A顺时针旋转120°,得到△ADC,点M是BO边上的一点,
∴AM=AM′,
∴AM′+DM的最小值=AM+DM的最小值,
作点D关于直线OB的对称点D′,连接AD′交OB于M,

则AD′=AM′+DM的最小值,
过D作DE⊥x轴于E,
∵∠OAD=120°,
∴∠DAE=60°,
∵AD=AO=3,
∴DE=![]() ×3=
×3=![]() ,AE=
,AE=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴D′( ![]() ,
,![]() ),
),
设直线AD′的解析式为y=kx+b,
∴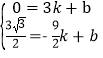 ,
,
∴
∴直线AD′的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴M(0,![]() ),
),
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,且PA=4,PB=![]() ,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③
,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③![]() ;④AB=
;④AB=![]() ;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有
;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有![]() 其中正确的有( )
其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中有点B(-2,0)和y轴上的动点A(0,a),其中a>0,以点A为直角顶点在第二象限内作等腰直角三角形ABC,设点C的坐标为(c,d).

(1)当a=4时,则点C的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=4时,在坐标平面内是否存在点P(不与点C重合),使△PAB与△ABC全等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O于点E,连接BE、CE.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,EF=4,DE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com