
【题目】如图,P是等边三角形ABC内一点,且PA=4,PB=![]() ,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③
,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③![]() ;④AB=
;④AB=![]() ;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有
;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有![]() 其中正确的有( )
其中正确的有( )

A.4个B.3个C.2个D.1个
【答案】B
【解析】
作BH⊥PC于H,根据等边三角形的性质得:BA=BC,∠ABC=60°,把△ABP绕点B顺时针旋转60°得到△CBD,证明出△PBD为等边三角形和△PCD为直角三角形即可求出①;根据平角性质,可得∠BPH=30°,证明△ABP为直角三角形,即可求出②和④;根据面积公式求出③;根据等面积法即可求出④.
作BH⊥PC于H
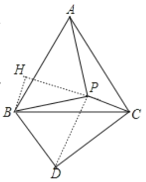
根据等边三角形的性质得:BA=BC,∠ABC=60°
把△ABP绕点B顺时针旋转60°得到△CBD,连接PD得到上图
根据旋转的性质可得CD=AP=4,BD=BP=![]() ,∠PBD=60°
,∠PBD=60°
∴△PBD为等边三角形
∴PD=PB=![]() ,∠BPD=60°
,∠BPD=60°
在三角形PDC中,PC=2,PD= ![]() ,CD=4
,CD=4
∴PC2+PD2=CD2
∴△PCD为直角三角形,∠CPD=90°
∴∠BPC=∠BPD+∠CPB=150°,故①错误;
根据平角性质,可得∠BPH=30°
在直角三角形PBH中,∵∠BPH=30°
∴PB=![]()
∴BH=![]() ,则PH=3
,则PH=3
CH=PC+PH=2+3=5
在直角三角形BCH中
![]() ,则
,则![]() ,故④正确;
,故④正确;
又∵![]()
∴△ABP为直角三角形,∠APB=90°
∴∠APC=360°-∠APB-∠BPC=120°,故选项②正确;
![]() ,故选项③错误;
,故选项③错误;
![]()
![]()
∴![]() ,故选项⑤正确
,故选项⑤正确
故答案选择:B.


科目:初中数学 来源: 题型:
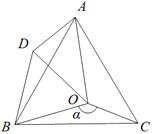
【题目】如图,点O是等边△ABC内一点,∠BOC=![]() ,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
(1) 求证:△BOD是等边三角形.
(2) 当![]() =150°时,试判断△AOD的形状,并说明理由.
=150°时,试判断△AOD的形状,并说明理由.
(3) 若△AOD是等腰三角形,请你直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x<3时,y1<y2;④当y1>0且y2>0时,﹣a<x<4.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:学习了分式运算后,老师布置了这样一道计算题:![]() ,甲、乙两位同学的解答过程分别如下:
,甲、乙两位同学的解答过程分别如下:
甲同学:
![]()
![]() ①
①
![]() ②
②
![]() ③
③
![]() ④
④
乙同学:
![]()
![]() ①
①
![]() ②
②
![]() ③
③
![]() ④
④
老师发现这两位同学的解答过程都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
(1)我选择________同学的解答过程进行分析. (填“甲”或“乙”)
(2)该同学的解答从第________步开始出现错误(填序号),错误的原因是________;
(3)请写出正确解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:已知方程x2+x﹣3=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x.所以x=![]() .
.
把x=![]() 代入已知方程,得(
代入已知方程,得(![]() )2+
)2+![]() ﹣3=0,化简,得y2+2y﹣12=0.
﹣3=0,化简,得y2+2y﹣12=0.
故所求方程为y2+2y﹣12=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的3倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
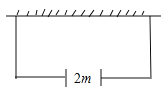
【题目】如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米?
(2)围成鸡场的面积可能达到200平方米吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )

A. (0,![]() ) B. (0,
) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,3)
) D. (0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三点在同一直线上,分别以AB、BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.

(1)求证:AE=CD;
(2)试判断△BMN的形状,并说明理由;
(3)设CD、AE相交于点G,求∠AGC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com