
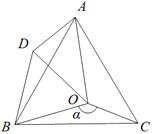
【题目】如图,点O是等边△ABC内一点,∠BOC=![]() ,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
(1) 求证:△BOD是等边三角形.
(2) 当![]() =150°时,试判断△AOD的形状,并说明理由.
=150°时,试判断△AOD的形状,并说明理由.
(3) 若△AOD是等腰三角形,请你直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)α=150°时,△AOD是直角三角形;理由见解析;(3)130°或100°或160°
【解析】
(1)根据旋转的性质可得出OB=BD,∠OBD=60°,根据等边三角形的判定即可求证;
(2)由(1)的结论可得∠BDO=60°;由于α=150°,所以∠ADB=∠BOC=150°,继而可得∠ADO=∠ADB-∠ODB=90°,由∠AOC=100°,∠BOD=60°,可求出∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,根据三角形的内角即可判定三角形的形状;
(3)分AO=AD、AO=OD、DO=AD三种情况,根据等腰三角形的概念,三角形内角和定理计算.
(1)证明:∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴BO=BD,∠OBD=60°,
∴△BOD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.理由是:
∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴△BOC≌△BDA,
∴∠ADB=∠BOC=150°,
又∵△BOD是等边三角形,
∴∠ODB=60°,
∴∠ADO=∠ADB-∠ODB=90°,
∵∠α=150°,∠AOC=100°,∠BOD=60°,
∴∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,
∴△AOD不是等腰直角三角形,
即△AOD是直角三角形.
(3) ∵△BOD是等边三角形,
∴∠ADO=α-60°,
∵OD=OA,
∴∠OAD=∠ODA=α-60°,
∴∠AOD=180°-2(α-60°),解得α=100°;
当OD=AD时,α+100°+60°+∠AOD=360°,
∠AOD=![]() ,解得α=160°;
,解得α=160°;
当OA=AD时,α+100°+60°+∠AOD=360°,∠AOD=α-60°,解得,α=130°
综合可得:130°或100°或160°


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
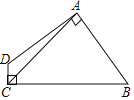
A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )

A. 以相同速度行驶相同路程,甲车消耗汽油最多
B. 以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C. 以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D. 以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)在图中作出△ABC关于x轴对称的图形△A1B1C1.
(2)作出△A1B1C1向左平移4个单位长度后得到的△A2B2C2,并直接写出点C2的坐标_____.
(3)△A2B2C2的面积是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,BD、CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,分别交AB、AC于E、F,则
,BD、CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,分别交AB、AC于E、F,则![]() 的周长为 ( )
的周长为 ( )

A.12B.13C.14D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,且PA=4,PB=![]() ,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③
,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③![]() ;④AB=
;④AB=![]() ;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有
;⑤点P到△ABC三边的距离分别为PE,PF,PG,则有![]() 其中正确的有( )
其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com