练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AC=BC，DC=EC，∠ACB=∠ECD=90°，且∠EBD=38°，则∠AEB=（ ）

    A.52°B.90°C.128°D.38°

    【答案】C

    【解析】

    先证明△BDC≌△AEC，进而得到角的关系，再由∠EBD的度数进行转化，最后利用三角形的内角和即可得到答案．

    ∵∠ACB＝∠ECD＝90°，
    ∴∠BCD＝∠ACE，
    在△BDC和△AEC中，
    ∵AC＝BC，∠BCD＝∠ACE，DC＝EC，
    ∴△BDC≌△AEC（SAS），
    ∴∠DBC＝∠EAC，
    ∵∠EBD＝∠DBC＋∠EBC＝38°，
    ∴∠EAC＋∠EBC＝38°，
    ∴∠ABE＋∠EAB＝90°－38°＝52°，
    ∴∠AEB＝180°－（∠ABE＋∠EAB）＝180°－52°＝128°，
    故答案为C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一辆摩拜单车放在水平的地面上，车把头下方A处与坐垫下方B处在平行于地面的水平线上，A、B之间的距离约为49cm，现测得AC、BC与AB的夹角分别为45°与68°，若点C到地面的距离CD为28cm，坐垫中轴E处与点B的距离BE为4cm，求点E到地面的距离（结果保留一位小数）．（参考数据：sin68°≈0.93，cos68°≈0.37，cot68°≈0.40）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

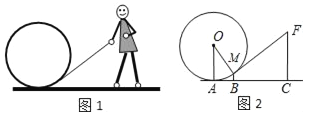
    【题目】图1是一个小朋友玩“滚铁环”的游戏，铁环是圆形的，铁环向前滚动时，铁环钩保持与铁环相切．将这个游戏抽象为数学问题，如图2．已知铁环的半径为25 cm，设铁环中心为O，铁环钩与铁环相切点为M，铁环与地面接触点为A，∠MOA=α，且sinα=．

    (1)求点M离地面AC的高度BM；

    (2)设人站立点C与点A的水平距离AC=55 cm，求铁环钩MF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一玩具工厂用于生产的全部劳力为450个工时，原料为400个单位．生产一个小熊要使用15个工时、20个单位的原料，售价为80元；生产一个小猫要使用10个工时、5个单位的原料，售价为45元．在劳力和原料的限制下合理安排生产小熊、小猫的个数，可以使小熊和小猫的总售价尽可能高．请用你所学过的数学知识分析，总售价是否可能达到2200元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

    （1）在图中的点上标出相应字母A、B、C，并求出△ABC的面积；

    （2）在图中作出△ABC关于y轴的对称图形△A1B1C1；

    （3）写出点A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学对九年级准备选考1分钟跳绳的同学进行测试，测试结果如下表：

    频数分布表：

    组别

    跳绳（次/1分钟）

    频数

    第1组

    190～199

    5

    第2组

    180～189

    11

    第3组

    170～179

    23

    第4组

    160～169

    33

    请回答下列问题：

    （1）此次测试成绩的中位数落在第　 　组中；

    （2）如果成绩达到或超过180次/分钟的同学可获满分，那么本次测试中获得满分的人数占参加测试人数的　 　%；

    （3）如果该校九年级参加体育测试的总人数为200人，若要绘制一张统计该校各项目选考人数分布的扇形图（如图），图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比，那么该扇形的圆心角应为　 　°；

    （4）如果此次测试的平均成绩为171次/分钟，那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在□ABCD中，点G为对角线AC的中点，过点G的直线EF分别交边AB、CD于点E、F，过点G的直线MN分别交边AD、BC于点M、N，且∠AGE=∠CGN.

    （1）求证：四边形ENFM为平行四边形；

    （2）当四边形ENFM为矩形时，求证：BE=BN.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解八年级学生一学期参加公益活动的时间情况，抽取50名八年级学生为样本进行调查，按参加公益活动的时间t（单位：小时），将样本分成五类：A类（0≤t≤2），B类（2＜t≤4），C类（4＜t≤6），D类（6＜t≤8），E类（t＞8），绘制成尚不完整的条形统计图．

    （1）样本中，E类学生有　 　人，请补全条形统计图；

    （2）该校八年级共600名学生，求八年级参加公益活动时间6＜t≤8的学生数；

    （3）从样本中选取参加公益活动时间在0≤t≤4的2人做志愿者，求这2人参加公益活动时间都在2＜t≤4中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

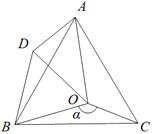
    【题目】如图，点O是等边△ABC内一点，∠BOC＝，∠AOC＝100°，将△BOC绕点B按逆时针方向旋转60°得到△BDA，连接OD.

    (1) 求证：△BOD是等边三角形.

    (2) 当＝150°时，试判断△AOD的形状，并说明理由.

    (3) 若△AOD是等腰三角形，请你直接写出的度数.

    查看答案和解析>>

    同步练习册答案