
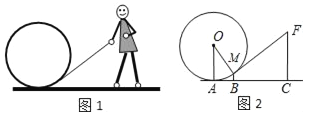
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
【答案】(1)BM=5cm;(2)MF=50cm.
【解析】
(1)过M作与AC平行的直线,与OA、FC分别相交于H、N.那么求BM的长就转化为求HA的长,而要求出HA,必须先求出OH,在直角三角形OHM中,sinα的值,且铁环的半径为5个单位即OM=5,可求得HM的值,从而求得HA的值;
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,又因为sin∠MOA=![]() ,所以可得出FN和FM之间的数量关系,即FN=
,所以可得出FN和FM之间的数量关系,即FN=![]() FM,再根据MN=HN-HM,利用勾股定理即可求出FM的长.
FM,再根据MN=HN-HM,利用勾股定理即可求出FM的长.
过M作与AC平行的直线,与OA、FC分别相交于H、N,
(1)在Rt△OHM中,∠OHM=90°,OM=25,
HM=OM×sinα=15,
所以OH=20,
MB=HA=25-20=5,
所以点M距地面的高度BM为5cm;
(2)∵铁环钩与铁环相切,
∴∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,
∴![]() =sin∠MOA=
=sin∠MOA=![]() ,
,
∴FN=![]() FM,
FM,
在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=55-15=40,
∵FM2=FN2+MN2,
即FM2=(![]() FM)2+402,
FM)2+402,
解得:FM=50,
∴铁环钩的长度FM为50cm.


科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP.
(1)求证:AB是⊙O的切线.
(2)若OA=4,则
①当![]() 长为_____时,四边形OECF是菱形;
长为_____时,四边形OECF是菱形;
②当![]() 长为_____时,四边形OCBP是正方形.
长为_____时,四边形OCBP是正方形.![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx–1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2–2x–1–t=0(t为实数)在–1<x<4的范围内有实数解,则t的取值范围是

A. t≥–2 B. –2≤t<7
C. –2≤t<2 D. 2<t<7
查看答案和解析>>
科目:初中数学 来源: 题型:
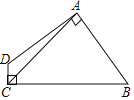
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=![]() (x>O)经过点C.
(x>O)经过点C.

(1)求b,k的值;
(2)求△BDC的面积;
(3)在反比例函数y=![]() (x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标.
(x>0)的图象上找一点P(异于点C),使△BDP与△BDC的面积相等,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为4×6的边长为1个单位的正方形网格,请在所给网格中按下列要求画顶点在格点的三角形.

(1)在图1中画△ABC,且AB=AC=![]() ,BC=
,BC=![]() ;
;
(2)在图2中画一个三边长均为无理数,且各边都不相等的直角△DEF(请注明各边长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com