
【题目】如图是规格为4×6的边长为1个单位的正方形网格,请在所给网格中按下列要求画顶点在格点的三角形.

(1)在图1中画△ABC,且AB=AC=![]() ,BC=
,BC=![]() ;
;
(2)在图2中画一个三边长均为无理数,且各边都不相等的直角△DEF(请注明各边长).
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
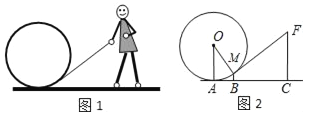
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一玩具工厂用于生产的全部劳力为450个工时,原料为400个单位.生产一个小熊要使用15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时、5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫的总售价尽可能高.请用你所学过的数学知识分析,总售价是否可能达到2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
频数分布表:
组别 | 跳绳(次/1分钟) | 频数 |
第1组 | 190~199 | 5 |
第2组 | 180~189 | 11 |
第3组 | 170~179 | 23 |
第4组 | 160~169 | 33 |
请回答下列问题:
(1)此次测试成绩的中位数落在第 组中;
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的 %;
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为 °;
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.

(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com