
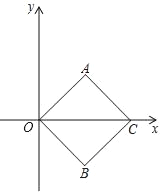
【题目】如图,四边形AOBC是正方形,点C的坐标是(4![]() ,0).
,0).
(Ⅰ)正方形AOBC的边长为 ,点A的坐标是 .
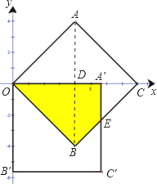
(Ⅱ)将正方形AOBC绕点O顺时针旋转45°,点A,B,C旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(Ⅲ)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时同时停止运动,当△OPQ为等腰三角形时,求出t的值(直接写出结果即可).
【答案】(1)4,![]() ;(2)旋转后的正方形与原正方形的重叠部分的面积为
;(2)旋转后的正方形与原正方形的重叠部分的面积为![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接AB,根据△OCA为等腰三角形可得AD=OD的长,从而得出点A的坐标,则得出正方形AOBC的面积;
(2)根据旋转的性质可得OA′的长,从而得出A′C,A′E,再求出面积即可;
(3)根据P、Q点在不同的线段上运动情况,可分为三种列式①当点P、Q分别在OA、OB时,②当点P在OA上,点Q在BC上时,③当点P、Q在AC上时,可方程得出t.
解:(1)连接AB,与OC交于点D,
四边形![]() 是正方形,
是正方形,
∴△OCA为等腰Rt△,
∴AD=OD=![]() OC=2
OC=2![]() ,
,
∴点A的坐标为![]() .
.
4,![]() .
.
(2)如图
∵ 四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵ 将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,
,
∴ 点![]() 落在
落在![]() 轴上.
轴上.
∴![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,
∴![]() .
.
∵ 四边形![]() ,
,![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
![]() ,
,
∴![]()
![]() .
.
∴旋转后的正方形与原正方形的重叠部分的面积为![]() .
.
(3)设t秒后两点相遇,3t=16,∴t=![]()
①当点P、Q分别在OA、OB时,
∵![]() ,OP=t,OQ=2t
,OP=t,OQ=2t
∴![]() 不能为等腰三角形
不能为等腰三角形
②当点P在OA上,点Q在BC上时如图2,
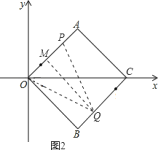
当OQ=QP,QM为OP的垂直平分线,
OP=2OM=2BQ,OP=t,BQ=2t-4,
t=2(2t-4),
解得:t=![]() .
.
③当点P、Q在AC上时,
![]() 不能为等腰三角形
不能为等腰三角形
综上所述,当![]() 时
时![]() 是等腰三角形
是等腰三角形


科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生200米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
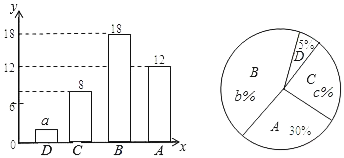
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答问题.
材料:求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型,此类题型试题有时出题者将圆隐藏,故又称为“隐圆问题”.解决这类问题,关键是要找到动点的运动轨迹,即该动点是绕哪一个定点旋转,且能保持旋转半径不变.从而找到动点所在的隐藏圆,进面转换成圆外一点到圆心的距离减半径,求得最小值.
解决问题:
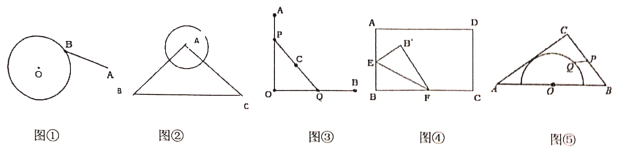
(1)如图①,圆O的半径为1,圆外一点A到圆心的距离为3,圆上一动点B,当A、O、B满足条件____________时,![]() 有最小值为____________.
有最小值为____________.
(2)如图②,等腰![]() 两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到
两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到![]() 的距离最小值为__________.
的距离最小值为__________.
(3)如图③,![]() ,P、Q分别是射线
,P、Q分别是射线![]() 、
、![]() 上两个动点,C是线段
上两个动点,C是线段![]() 的中点,且
的中点,且![]() ,则在线段
,则在线段![]() 滑动的过程中,求点C运动形成的路径长,并说明理由.
滑动的过程中,求点C运动形成的路径长,并说明理由.
(4)如图④,在矩形![]() 中,
中,![]() ,
,![]() ,点E是
,点E是![]() 中点,点F是
中点,点F是![]() 上一点,把
上一点,把![]() 沿着
沿着![]() 翻折,点B落在点
翻折,点B落在点![]() 处,求
处,求![]() 的最小值,并说明理由.
的最小值,并说明理由.
(5)如图⑤,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 中点O为圆心,作半圆与
中点O为圆心,作半圆与![]() 相切,点P,Q分别是边
相切,点P,Q分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,求
,求![]() 长的最小值,并说明理由.
长的最小值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
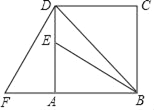
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为
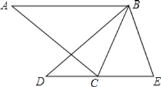
A. 36° B. 40° C. 45° D. 50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com