
【题目】如图, ![]() ABCD中,EF⊥CD交BD于点G,∠ECF=∠DGF,DG=CE,求证:四边形ABCD是菱形.
ABCD中,EF⊥CD交BD于点G,∠ECF=∠DGF,DG=CE,求证:四边形ABCD是菱形.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP=5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
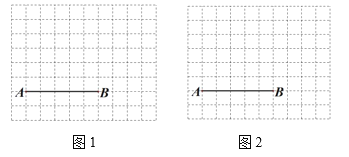
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(3)班学生的家距离学校人数的频数分布直方图如图所示,则下列说法中不正确的一项是( )
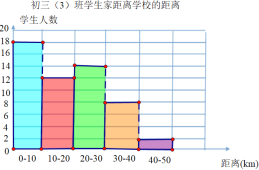
A.初三(3)班共有54名学生,其中家距离学校20-30km的学生人数为中位数.
B.初三(3)班学生的家距离学校为0-10km的学生人数的组中值为5km
C.初三(3)班学生的家距离学校为0-10km的学生人数为众数
D.初三(3)班学生的家距离学校各组数据的组中值的平均数为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3a-5经过点A(2,5)
(1)求出a和b之间的数量关系.
(2)已知抛物线的顶点为D点,直线AD与y轴交于(0,-7)
①求出此时抛物线的解析式;
②点B为y轴上任意一点且在直线y=5和直线y=-13之间,连接BD绕点B逆时针旋转90°,得到线段BC,连接AB、AC,将AB绕点B顺时针旋转90°,得到线段BH.截取BC的中点F和DH的中点G.当点D、点H、点C三点共线时,分别求出点F和点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
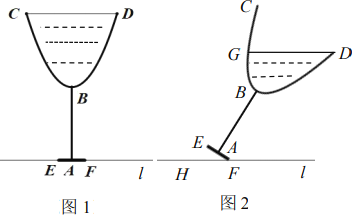
【题目】图1是一个高脚杯截面图,杯体![]() 呈抛物线状(杯体厚度不计),点
呈抛物线状(杯体厚度不计),点![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,点
,点![]() 是
是![]() 的中点,当高脚杯中装满液体时,液面
的中点,当高脚杯中装满液体时,液面![]() ,此时最大深度(液面到最低点的距离)为
,此时最大深度(液面到最低点的距离)为![]() ,将高脚杯绕点
,将高脚杯绕点![]() 缓缓倾斜倒出部分液体,当
缓缓倾斜倒出部分液体,当![]() 时停止,此时液面为
时停止,此时液面为![]() ,则液面
,则液面![]() 到平面
到平面![]() 的距离是________________;此时杯体内液体的最大深度为_____________________.
的距离是________________;此时杯体内液体的最大深度为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
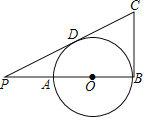
A.1.5B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右边)交
的右边)交![]() 轴于点
轴于点![]() ,
,![]() .
.
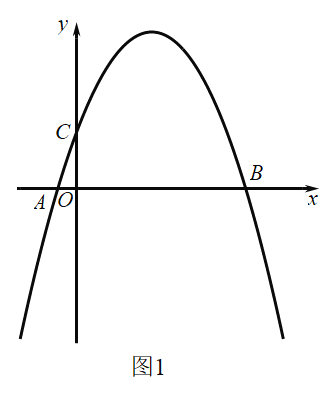
(1)如图1,求抛物线的解析式;
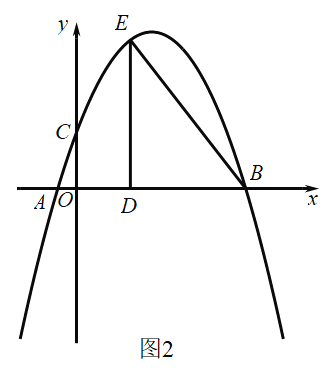
(2)如图2,点![]() 是第一象限抛物线上的点,连接
是第一象限抛物线上的点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
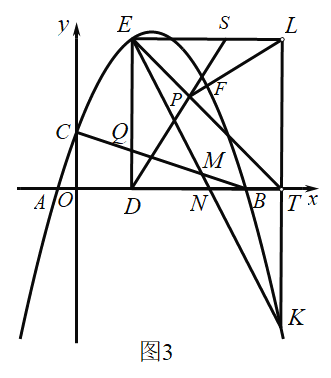
(3)如图3,在(2)的条件下,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是第四象限抛物线上的点,连接
是第四象限抛物线上的点,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,点
,点![]() 是抛物线对称轴右侧第一象限抛物线上的点,连接
是抛物线对称轴右侧第一象限抛物线上的点,连接![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com