
【题目】如图,直线y=2x+3与反比例函数y=![]() 的图像相交于点B(a,5),且与x轴相交于点A
的图像相交于点B(a,5),且与x轴相交于点A

(1)求反比例函数的表达式.
(2)若P为反比例函数图像上一点,且△AOP的面积是△AOB的面积的![]() ,请求出点P的坐标.
,请求出点P的坐标.
【答案】(1)![]() (2)(2,
(2)(2,![]() )或(-2,-
)或(-2,-![]() )
)
【解析】
(1)根据待定系数法可代入求解a;然后代入求出k的值;
(2)设点P的坐标为(0,m),令直线y=2x+3中的y=0,解得x的值,得到A点的坐标,利用三角形的面积公式,结合面积之间的关系即可得出关于m的方程,解方程即可.
试题解析:(1)解:∵点B(a,5)在直线y=2x+3上,
∴2a+3=5,∴a=1.
∴B(1,5)在反比例函数y![]() 的图像上,
的图像上,
∴k=1×5=5.∴反比例函数的表达式为y![]() .
.
(2)设点P的坐标为(m, ![]() ),令直线y=2x+3中的y=0,解得x=
),令直线y=2x+3中的y=0,解得x=![]()
则点A的坐标为(![]() ,0)
,0)
∴△AOB的面积为: ![]()
∵△AOP的面积是△AOB的面积的![]()
∴△BOP的面积为![]()
解得m=±2
所以P点的坐标为:(2,![]() )或(-2,-
)或(-2,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况(每人限选一项),对全市部分九年级男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市九年级毕业学生中有5500名男生,试估计全市九年级男生中选“50米跑”的人数有多少人?
(3)甲、乙两名九年级男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球和立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暖羊羊有5张写着不同数字的卡片,请你按要求选择卡片,完成下列各问题:
![]()
(1)从中选择两张卡片,使这两张卡片上数字的乘积最大.
这两张卡片上的数字分别是 ,积为 _.
(2)从中选择两张卡片,使这两张卡片上数字相除的商最小.
这两张卡片上的数字分别是 ,商为 .
(3)从中选择4张卡片,每张卡片上的数字只能用一次,选择加、减、乘、除中的适当方法(可加括号),使其运算结果为24,写出运算式子.(写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。
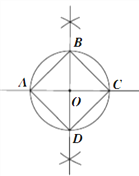
请回答:该尺规作图的依据是____________________________。(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知 RtABC 中,![]() ,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(-2,0).
(1)填空:c= (用含b的式子表示)。
(2)若b<4
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),直接写出b的取值范围为 ;
(3)直线y=x-4经过抛物线y=x2+bx+c的顶点P,求抛物线的表达式。
查看答案和解析>>
科目:初中数学 来源: 题型:
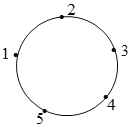
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com