等腰三角形的底边长为10cm.周长为36cm.则底角的正切值是( )A．$\frac{12}{5}$B．$\frac{5}{13}$C．$\frac{5}{12}$D．无法确定题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

15．等腰三角形的底边长为10cm，周长为36cm，则底角的正切值是（　　）

A．

$\frac{12}{5}$

B．

$\frac{5}{13}$

C．

$\frac{5}{12}$

D．

无法确定

分析根据等腰三角形的周长，底边长，可得腰长，根据勾股定理，可得底边上的高，根据正切函数的定义，可得答案．

解答解：如图，△ABC中，AB=AC，BC=10cm，周长为36cm，
则AB=AC=（36-10）÷2=13cm．
作AD⊥BC于D点，则BD=CD=5cm，
由勾股定理得，AD=12cm，
所以底角的正切值tan∠ABC=$\frac{AD}{BD}$=$\frac{12}{5}$．
故选A．

点评此题主要考查了解直角三角形，等腰三角形的性质，锐角三角函数的定义，利用勾股定理求出底边上的高是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

5．某公司销售一种进价为20（元/个）的计算器，其销售量y（万个）与销售价格x（元/个）之间为一次函数关系，其变化如下表：

价格x （元/个）	…	30	50	…
销售量y （万个）	…	5	3	…

同时，销售过程中的其他开支（不含进价）总计40万元．若该公司要获得40万元的净利润，且尽可能让顾客得到实惠，那么销售价格应定为多少？
（注：净利润=总销售额-总进价-其他开支）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．当x取何值时，整式$\frac{x-1}{2}$+$\frac{2x+1}{6}$的值比$\frac{x-1}{3}$的值大1？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

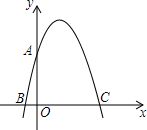如图，在平面直角坐标系中，点0为坐标原点，抛物线y=ax²+bx+4与y轴交于点A，与x轴交于点B、C（点B在点C左侧），且OA=OC=4OB．
（1）求a，b的值；
（2）连接AB、AC，点P是抛物线上第一象限内一动点，且点P位于对称轴右侧，
过点P作PD⊥AC于点E，分别交x、y轴于点D、H，过点P作PG∥AB交AC于点F，交x轴于点G，设P（x，y），线段DG的长为d，求d与x之间的函数关系（不要求写出自变量x的取值范围）；
（3）在（2）的条件下，当$\frac{{{S_{△PEF}}}}{{{S_{△PDF}}}}=\frac{3}{8}$时，连接AP并延长至点M，连接HM交AC于点S，点R是抛物线上一动点，当△ARS为等腰直角三角形时．求点R的坐标和线段AM的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

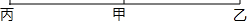甲、乙、丙三地位置如图所示，甲、乙两地相距30km，丙地离甲地足够远，小明骑自行车从甲地往丙地，小军骑自行车从乙地往丙地，小明的速度为5km/h，小军的速度为15km/h．问：两人同时出发多长时间后相距20km？