
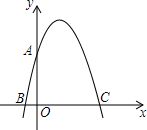
 如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.分析 (1)将x=0代入求得y=4,从而得到点A的坐标为(0,4),由OA=OC=4OB可求得C(4,0),B(-1,0),然后将点B、C的坐标代入抛物线的解析式可求得a=-1,b=3;
(2)作PK⊥x轴于点K.由题意可知△AOC为等腰直角三角形,于是得到∠ACO=45°,由AC⊥PD可证明∠EDC=45°,从而得到△PDK为等腰直角三角形,故此PK=DK=y,由AB∥PG可知∠ABO=∠PGK,由锐角三角函数的定义可知$\frac{AO}{OB}$=$\frac{PK}{GK}$=4,从而得到GK=$\frac{1}{4}$PK=$\frac{1}{4}$y,由d=DK-GK可求得d=$-\frac{3}{4}{x^2}+\frac{9}{4}x+3$;
(3)如图2所示:过点P作PK⊥x轴,垂足为K,PK交于AC与N.由题意可知:$\frac{PE}{PD}=\frac{3}{8}$,设点P的坐标为(x,y),由△NKC为等腰直角三角形可知CK=NK=4-x,由PN=PK-KN可知PN=y-4+x,由△PEN为等腰三角三角形可知PE=$\frac{{\sqrt{2}}}{2}PN$=$\frac{{\sqrt{2}}}{2}(y-4+x)$,由△PBK为等腰直角三角形可知PD=$\sqrt{2}PK$=$\sqrt{2}y$,从而可得到$\frac{{\frac{{\sqrt{2}}}{2}(y-4+x)}}{{\sqrt{2}y}}=\frac{3}{8}$,$\frac{y-4+x}{2y}=\frac{3}{8}$,将y=-x2+3x+4代入得:$\frac{-{x}^{2}+4x}{2(-{x}^{2}+3x+4)}=\frac{3}{8}$.解得:x1=3,x2=4(舍去)于是可求得P(3,4),从而得打D(-1,0),故此点D、B重合,由△BOH为等腰直角三角形,可求得AH=3.如图3所示:∠RAS=90°时.设点R(a,-a2+3a+4)由△ARS为等腰直角三角形,可证明RS⊥AM,从而得到AL=LS,AL=LR,故此a=-a2+3a+4-4可求得R(2,6).由锐角三角函数的定义可知:$\frac{LS}{LM}$=$\frac{AH}{AM}$,从而得到$\frac{2}{LM}=\frac{3}{2+LM}$,解得LM=4,于是可求得AM=6;当∠ARS=90°和∠ASR=90°时,△ARS不能构成等腰直角三角形,故此AM的长为6.
解答 解:(1)y=ax2+bx+4,当x=0时,y=4,
∴A(0,4)
∵OC=OA=4OB,
∴OC=4,OB=1,
∴C(4,0),B(-1,0)
将C(4,0),B(-1,0)代入抛物线y=ax2+bx+4
得:$\left\{{\begin{array}{l}{16a+4b+4=0}\\{a-b+4=0}\end{array}}\right.$,解得:$\left\{{\begin{array}{l}{a=-1}\\{b=3}\end{array}}\right.$
∴a=-1 b=3.
(2)如图1,作PK⊥x轴于点K.
∵a=-1 b=3.
∴抛物线的解析式为y=-x2+3x+4.
设点P的坐标为(x,y)
∵OA=OC,∠AOC=90°,
∴∠ACO=45°,
∵AC⊥PD,
∴∠EDC=45°,
∵PK⊥x轴,
∴△PDK为等腰直角三角形,
∴PK=DK=y,
∵AB∥PG,
∴∠ABO=∠PGK,
∵tan∠ABO=$\frac{AO}{OB}$=4,
∴tan∠PGK=$\frac{PK}{GK}$=4
∴GK=$\frac{1}{4}$PK=$\frac{1}{4}$y
∴d=DK-GK=y-$\frac{1}{4}$y=$\frac{3}{4}$y,
将y=-x2+3x+4代入得:d=$\frac{3}{4}$(-x2+3x+4)=$-\frac{3}{4}{x^2}+\frac{9}{4}x+3$.
(3)如图2所示:过点P作PK⊥x轴,垂足为K,PK交于AC与N.
∵$\frac{{{S_{△PEF}}}}{{{S_{△PDF}}}}=\frac{3}{8}$
∴$\frac{PE}{PD}=\frac{3}{8}$.
设点P的坐标为(x,y).
∵CK=NK=4-x
∴PN=y-4+x
∴PE=$\frac{{\sqrt{2}}}{2}PN$=$\frac{{\sqrt{2}}}{2}(y-4+x)$,PD=$\sqrt{2}PK$=$\sqrt{2}y$
∴$\frac{{\frac{{\sqrt{2}}}{2}(y-4+x)}}{{\sqrt{2}y}}=\frac{3}{8}$,$\frac{y-4+x}{2y}=\frac{3}{8}$.
将y=-x2+3x+4代入得:$\frac{-{x}^{2}+4x}{2(-{x}^{2}+3x+4)}=\frac{3}{8}$.
整理得:x2-7x+12=0.
解得:x1=3,x2=4(舍去).
∴P(3,4)
∵DK=PK=4,
∴D(-1,0).
∴点D、B重合.
∵△BOH为等腰直角三角形,
∴OH=OB=1.
∴AH=3.
如图3所示:∠RAS=90°时.
设点R(a,-a2+3a+4)
∵△ARS为等腰直角三角形
∴∠RAS=90°,∠ARS=45°
∵AP∥x轴
∴∠PAC=∠ACO=45°.
∴∠RAP=45°.
∴RS⊥AM.
∴AL=LS,AL=LR.
∴a=-a2+3a+4-4.
∴a=2.
∴R(2,6).
在Rt△LMS中tan∠M=$\frac{LS}{LM}$,在Rt△AHM中tan∠M=$\frac{AH}{AM}$
∴$\frac{LS}{LM}$=$\frac{AH}{AM}$.
∴$\frac{2}{LM}=\frac{3}{2+LM}$
∴LM=4
∴AM=6.
当∠ARS=90°和∠ASR=90°时,△ARS不能构成等腰直角三角形.
综上所述,AM的长为6.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、等腰直角三角形的性质和判定、特殊锐角三角函数值、锐角三角函数的定义,根据等腰直角三角形的性质列出关于x和LM的方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画出函数y=-3x+2的图象.
画出函数y=-3x+2的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
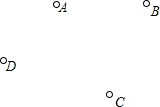 已知平面上有四个点,按要求画图:
已知平面上有四个点,按要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com