
 画出函数y=-3x+2的图象.
画出函数y=-3x+2的图象.分析 (1)直接把点代入函数解析式判定即可;
(2)分别令x=0,y=0求得直线与坐标轴的交点坐标,然后结合三角形的面积计算方法求得答案即可.
解答 解:如图,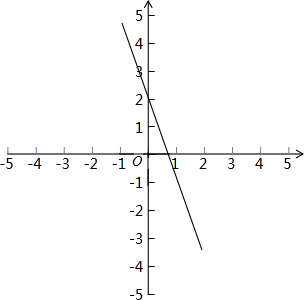
(1)当x=2时,y=-3x+2=-4,点P(2,5)不在此函数的图象上;
(2)令x=0时,y=2,则此直线与y轴交点的坐标为(0,2);
令y=0时,x=$\frac{2}{3}$,则此直线与x轴交点的坐标为($\frac{2}{3}$,0);
直线与坐标轴所围成的三角形面积=$\frac{1}{2}$×2×$\frac{2}{3}$=$\frac{2}{3}$.
点评 本题考查了一次函数图象上点的坐标特征,以及点与函数图象的关系,在函数图象上则满足函数解析式,不在图象上,则不满足函数解析式.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
| 价格x (元/个) | … | 30 | 50 | … |
| 销售量y (万个) | … | 5 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
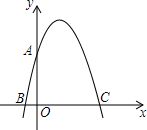 如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示
用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com