
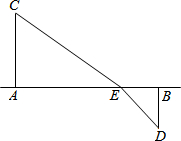
 如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时
如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时分析 (1)根据勾股定理分别用含x的代数式来表示CE和DE,二者相加即可得出结论;
(2)连接CD,由CA⊥AB于点A,DB⊥AB于点B可得出△CAE∽△DBE,根据相似三角形的性质可得出$\frac{AE}{BE}=\frac{CA}{DB}$,找出AE长度即可找出E点的位置;
(3)过点C作CC′∥AB,延长DB交CC′与点C′,结合(2)的结论即可得出结论.
解答 解:(1)∵AE=x,AB=25,
∴BE=25-x.
由勾股定理可得:
CE=$\sqrt{A{C}^{2}+A{E}^{2}}$=$\sqrt{225+{x}^{2}}$,DE=$\sqrt{D{B}^{2}+B{E}^{2}}$=$\sqrt{100+(25-x)^{2}}$.
∴CE+DE=$\sqrt{225+{x}^{2}}$+$\sqrt{100+(25-x)^{2}}$.
(2)连接CD,如图1所示.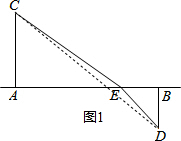
当点E为AB与CD的交点时,CE+DE最短.
∵CA⊥AB于点A,DB⊥AB于点B,
∴∠CAE=∠DBE=90°,
又∵∠CEA=∠DEB,
∴△CAE∽△DBE,
∴$\frac{AE}{BE}=\frac{CA}{DB}$,即$\frac{x}{25-x}=\frac{15}{10}$,
解得:x=15.
∴当点E离点A15km时,CE+DE的长最短.
(3)过点C作CC′∥AB,延长DB交CC′与点C′,如图2所示.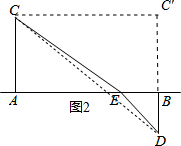
CD=$\sqrt{CC{′}^{2}+DC{′}^{2}}$=$\sqrt{A{B}^{2}+(AC+DB)^{2}}$.
结合(2)的结论可知:
当$\frac{x}{24-x}=\frac{\sqrt{9}}{\sqrt{16}}$时,$\sqrt{{x}^{2}+9}$$+\sqrt{(24-x)^{2}+16}$最小.
解$\frac{x}{24-x}=\frac{\sqrt{9}}{\sqrt{16}}$得,x=$\frac{72}{7}$.
此时$\sqrt{{x}^{2}+9}$$+\sqrt{(24-x)^{2}+16}$=$\sqrt{2{4}^{2}+(3+4)^{2}}$=25.
点评 本题考查了最短线路问题、勾股定理以及相似三角形的判定及性质,解题的关键是:(1)利用勾股定理找出线段的长;(2)由相似三角形的性质找出E点的位置;(3)由勾股定理得出结论.本题属于中档题,难度不大,解决该题型题目时,巧妙的利用构建直角三角形,结合勾股定理得出结论.


科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O直径,CD为弦,弦CD⊥AB于点M,F为DC延长线上一点,连接CE、AD、AF,AF交⊙O于E,连接ED交AB于N.
如图,AB为⊙O直径,CD为弦,弦CD⊥AB于点M,F为DC延长线上一点,连接CE、AD、AF,AF交⊙O于E,连接ED交AB于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )| A. | $\sqrt{29}$ | B. | $\sqrt{37}$ | C. | $\sqrt{21}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
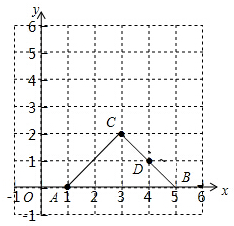 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
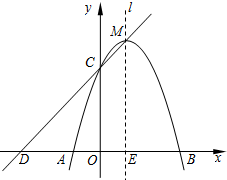 如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com