

���� [��֪]����AF�����۵������ʿɵ�AB=AG=AD���ٽ��AFΪ��AGF�͡�ADF�Ĺ����ߣ��Ӷ�֤����AGF�ա�ADF���Ӷ��ó�����FD=FG��
[̽��]����AF������ͼ�β���FD=FG�����۵������ʿɵ�AB=AG=AD���ٽ��AFΪ��AGF�͡�ADF�Ĺ����ߣ��Ӷ�֤����AGF�ա�ADF���Ӷ��ó����ۣ�
[Ӧ��]��AB=x����BE=EG=x-5��FE=x-2��FC=x-3����RT��ECF�����ù��ɶ��������x��ֵ�������ɵó��𰸣�
���  [��֪]�⣺����FD=FG��
[��֪]�⣺����FD=FG��
֤������ͼ1������AF��
���۵������ʿɵ�AB=AG=AD��
��Rt��AGF��Rt��ADF��
$\left\{\begin{array}{l}{AG=AD}\\{AF=AF}\end{array}\right.$��
��Rt��AGF��Rt��ADF��HL����
�ʿɵ�FG=FD��
[̽��]�⣺����FD=FG��
֤������ͼ2������AF��
���۵������ʿɵ�AB=AG=AD��
��Rt��AGF��Rt��ADF��
$\left\{\begin{array}{l}{AG=AD}\\{AF=AF}\end{array}\right.$��
��Rt��AGF��Rt��ADF��HL����
�ʿɵ�FG=FD��
[Ӧ��]��AB=x����BE=EG=x-5��FE=x-2��FC=x-3��
��Rt��ECF��EF2=FC2+EC2������x-2��2=��x-3��2+52��
���x=15��
��AB�ij�Ϊ15��
���� ���⿼���˷��۱任�������ε����ʣ����ա�AGF�ա�ADFʼ�ղ����ǽ����Ĺؼ��������ڽ��н��۵�Ӧ��ʱ���ó�Rt��EFC�ĸ��ߺ����ù��ɶ����������ʱ��Ҫϸ�ı��������


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6��4 | B�� | -8��14 | C�� | -6��6 | D�� | -8��-14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
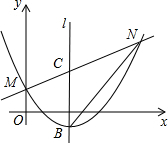 ��ͼ��ֱ��y=$\frac{1}{2}$x+1��������y=$\frac{1}{2}$x2-bx+l���ڲ�ͬ������M��N����M�ڵ�N����ࣩ��
��ͼ��ֱ��y=$\frac{1}{2}$x+1��������y=$\frac{1}{2}$x2-bx+l���ڲ�ͬ������M��N����M�ڵ�N����ࣩ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
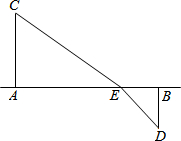 ��ͼ��ʾ��·��A��B��վ����Ϊ�����㣩���25km��C��DΪ����ׯ����Ϊ�����㣩��CA��AB�ڵ�A��DB��AB�ڵ�B����֪CA=15km��DB=10km����Ҫ��A��B֮�佨һ�����ز��չ�վE����AE=xkmʱ
��ͼ��ʾ��·��A��B��վ����Ϊ�����㣩���25km��C��DΪ����ׯ����Ϊ�����㣩��CA��AB�ڵ�A��DB��AB�ڵ�B����֪CA=15km��DB=10km����Ҫ��A��B֮�佨һ�����ز��չ�վE����AE=xkmʱ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
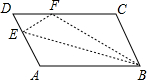 ��ͼ��ƽ���ı���ABCD�У���E�ڱ�AD�ϣ���BEΪ�ۺۣ�����ABE�۵���ʹ��A������CD�ϵ�F���غϣ�����FDE���ܳ�Ϊ16����FCB���ܳ�Ϊ28����FC�ij�Ϊ6��
��ͼ��ƽ���ı���ABCD�У���E�ڱ�AD�ϣ���BEΪ�ۺۣ�����ABE�۵���ʹ��A������CD�ϵ�F���غϣ�����FDE���ܳ�Ϊ16����FCB���ܳ�Ϊ28����FC�ij�Ϊ6���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com