
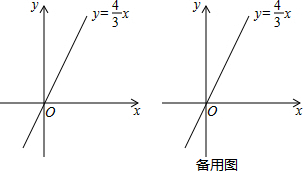
分析 (1)由抛物线的解析式可得出抛物线对称轴为x=3,将x=3代入直线AB的解析式中即可求出点C的坐标;由抛物线的解析式表示出顶点坐标,结合两点间的距离公式即可得出CD的长度;
(2)将直线解析式代入抛物线解析式中,得出关于x的二元一次方程,由求根公式找出x值中较大的数,令其为t,变换等式即可得出结论;
(3)①借用(2)的结论,利用CD=CB得出关于m的一元二次方程,解方程得出m的值代入原方程进行验证即可确定m的结果,在将m代入t关于m的解析式中即可得出B点的横坐标,由点B在直线y=$\frac{4}{3}$x上即可得出B点坐标;②作B点关于对称轴的对称点B′,过点F作FM⊥BC于点M,连接B′M,通过三角形内两边之和大于第三边找出点F的位置,再结合两直线垂直,斜率之积为-1找出B′M的解析式,结合对称轴为x=3即可得出结论.
解答 解:(1)抛物线y=(x-3)2-4m+3的对称轴为x=3,
令x=3,则有y=$\frac{4}{3}$×3=4,
即点C的坐标为(3,4).
抛物线y=(x-3)2-4m+3的顶点D的坐标为(3,-4m+3),
∵点D在点C的下方,
∴CD=4-(-4m+3)=4m+1.
(2)∵点B在直线y=$\frac{4}{3}x$上,且其横坐标为t,
则点B的坐标为(t,$\frac{4}{3}$t),
将点B的坐标代入抛物线y=(x-3)2-4m+3中,
得:$\frac{4}{3}$t=(t-3)2-4m+3,
整理,得:m=$\frac{1}{4}{t}^{2}$-$\frac{11}{6}$t+3.
(3)①依照题意画出图形,如图1所示.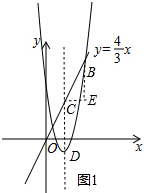
过点C作CE∥x轴,过点B作BE∥y轴交CE于点E.
∵直线BC的解析式为y=$\frac{4}{3}$x,
∴BE=$\frac{4}{3}$CE,
由勾股定理得:BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=$\frac{5}{3}$CE.
∵CD=CB,
∴有4m+1=$\frac{5}{3}$(t-3)=$\frac{5}{3}$($\frac{11}{3}$+$\sqrt{\frac{13}{9}+4m}$-3),
解得:m=-4,或m=1.
当m=-4时,$\frac{13}{9}$+4×(-4)=-$\frac{131}{9}$<0,不合适,
∴m=1,
此时t=$\frac{11}{3}$+$\sqrt{\frac{13}{9}+4}$=6,
y=$\frac{4}{3}$×6=8.
故此时点B的坐标为(6,8).
②作B点关于对称轴的对称点B′,过点F作FM⊥BC于点M,连接B′M.
∵直线BC的解析式为y=$\frac{4}{3}$,FM⊥BC,
∴tan∠FCM=$\frac{1}{\frac{4}{3}}$=$\frac{3}{4}$,
∴sin∠FCM=$\frac{FM}{FC}=\frac{3}{5}$.
∵B、B′关于对称轴对称,
∴BF=B′F,
∴BF+$\frac{3}{5}$CF=B′F+FM.
当点B′、F、M三点共线时B′F+FM最小.
∵B点坐标为(6,8),抛物线对称轴为x=3,
∴B′点的坐标为(0,8).
又∵B′M⊥BC,
∴直线B′M的斜率为$\frac{-1}{\frac{4}{3}}$=-$\frac{3}{4}$,
∴直线B′M的解析式为y=-$\frac{3}{4}$x+8,
当x=3时,有y=-$\frac{3}{4}$×3+8=$\frac{23}{4}$.
即此时点F的坐标为(3,$\frac{23}{4}$).
故答案为:(3,$\frac{23}{4}$).
点评 本题考查了二次函数的性质、一元二次方程的求根公式、解直角三角形以及解无理方程,解题的关键是:(1)根据二次函数的解析式找出其对称轴及顶点坐标;(2)由求根公式得出t;(3)①得出关于m的无理方程;②寻到点F的位置.本题属于中档题,(1)(2)难度不大,(3)难度不小,①中涉及到了解无理方程,产生了增根需要去验证;②寻找F点的位置是关键,此处在直角三角形中利用了角的三角函数值寻找到点F的位置.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,A(-3,0),B(0,-4),C(4$\sqrt{3}$,0),D(0,4),点P、Q分别是线段AD、BC上的动点,AQ与BP交于点E,与y轴交于点F,∠BAD=180°-∠BEQ,设AP的长为x.
如图,在平面直角坐标系中,A(-3,0),B(0,-4),C(4$\sqrt{3}$,0),D(0,4),点P、Q分别是线段AD、BC上的动点,AQ与BP交于点E,与y轴交于点F,∠BAD=180°-∠BEQ,设AP的长为x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
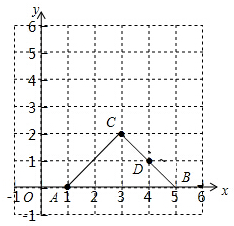 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
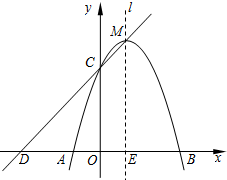 如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com