
 如图,在平面直角坐标系中,A(-3,0),B(0,-4),C(4$\sqrt{3}$,0),D(0,4),点P、Q分别是线段AD、BC上的动点,AQ与BP交于点E,与y轴交于点F,∠BAD=180°-∠BEQ,设AP的长为x.
如图,在平面直角坐标系中,A(-3,0),B(0,-4),C(4$\sqrt{3}$,0),D(0,4),点P、Q分别是线段AD、BC上的动点,AQ与BP交于点E,与y轴交于点F,∠BAD=180°-∠BEQ,设AP的长为x.分析 (1)由勾股定理得到AD=AB=5,再由△BGD∽△AOD,得到$\frac{BG}{OA}$=$\frac{BD}{AD}$,求出BG,再利用锐角的三角函数即可求解;
(2)先判断出△APE∽△AEP,得到FD=$\frac{21}{4}$,再判断出△EFB∽△BFA得到比例式求出AE=$\frac{12}{13}$,再由△APH∽△ADO求出AH,即可求解;
(3)分三种情况①当PA=EA时,由△APE≌△AFD求出AF,②当AP=PE时,由反证法判断不存在,③当AE=PE时,由△BKQ∽△BOC,通过计算即可.
解答 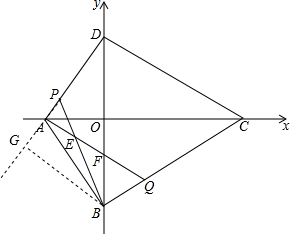 解:(1)如图,作BG⊥DA,交DA的延长线于G,
解:(1)如图,作BG⊥DA,交DA的延长线于G,
∵A(-3,0),B(0,-4),C(4$\sqrt{3}$,0),D(0,4),
∴OA=3,OD=0B=4,AC=8,
∴AD=AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠BGD=∠AOD=90°,∠BDG=∠ADO,
∴△BGD∽△AOD,
∴$\frac{BG}{OA}$=$\frac{BD}{AD}$,
∴BG=$\frac{OA•BD}{AD}$=$\frac{3×8}{5}$=$\frac{24}{5}$,
∴sin∠GAB=$\frac{BG}{AB}$=$\frac{\frac{24}{5}}{5}$=$\frac{24}{25}$,
∵∠BAD=180°-∠BEQ,
∴∠BEQ=180°-∠BAD=∠GAB,
∴sin∠BEQ=$\frac{24}{25}$;
(2)∵∠AEP=∠ADF,∠PAE=∠FAD,
∴△APE∽△AEP,
∴$\frac{AD}{DF}=\frac{AE}{DE}=\frac{20}{21}$
∴FD=$\frac{21}{20}$×AD=$\frac{21}{20}$×5=$\frac{21}{4}$,
∵BF=8-$\frac{21}{4}$=$\frac{11}{4}$,
∴OF=4-$\frac{11}{4}$=$\frac{5}{4}$,
∴AF=$\sqrt{{3}^{2}{+(\frac{5}{4})}^{2}}$=$\frac{13}{4}$,
∵∠FEB=∠FBA,∠EFB=BFA,
∴△EFB∽△BFA,
∴$\frac{EF}{FB}=\frac{FB}{FA}$,
∴EF=$\frac{11}{4}×\frac{11}{4}÷\frac{13}{4}$=$\frac{121}{52}$,
∴AE=$\frac{13}{4}$-$\frac{121}{52}$=$\frac{12}{13}$,
∵△APE∽△AFP,
∴$\frac{AP}{AE}=\frac{AF}{AD}$$\frac{AP}{AE}=\frac{AF}{AO}$,
∴AP=$\frac{3}{5}$,
作PH⊥x轴,
∴△APH∽△ADO,
∴$\frac{\frac{3}{5}}{PH}=\frac{5}{4}$,
∴$\frac{AH}{\frac{3}{5}}=\frac{3}{5}$,
∴PH=$\frac{12}{25}$,AH=$\frac{9}{25}$,HO=$\frac{66}{25}$,
∴P($\frac{66}{25}$,$\frac{12}{25}$).
(3)①当PA=EA时,
∵△APE≌△AFD,
∴AF=AD=5,
此时点F,Q重合,BQ=1,
②当AP=PE时,
有FA=FD,
∴∠FAD=∠ADF,
∵点Q在BC上,
∴∠FAD≥∠OAD,
∵OD=4>OA=3,
∴∠OAD>∠ADF,
∴∠FAD>∠ADF,
FA<AD,相矛盾,
∴AP≠PE;
③当AE=PE时,
∴DF=AD=5,FB=3,OF=1,
作QK⊥y轴,设KQ=x,
∵△QKF∽△AOF,
∴$\frac{KQ}{KF}=\frac{AO}{OF}$,
∴$\frac{x}{KF}=\frac{3}{1}$,
∴KF=$\frac{1}{3}$x,
∵△BKQ∽△BOC,
∴$\frac{BK}{KQ}=\frac{BO}{OC}$,
∴$\frac{BK}{x}=\frac{4}{4\sqrt{3}}$,
∴BK=$\frac{1}{\sqrt{3}}$x,
∵BF=BK+KF,
∴3=$\frac{1}{3}$x+$\frac{1}{\sqrt{3}}$x,
∴x=$\frac{9(\sqrt{3}-1)}{2}$;
∴KB=$\frac{1}{\sqrt{3}}$x=$\frac{1}{\sqrt{3}}$×$\frac{9(\sqrt{3}-1)}{2}$=$\frac{3(3-\sqrt{3})}{2}$,
∵BQ2=[$\frac{9(\sqrt{3}-1)}{2}$]2+[$\frac{3(3-\sqrt{3})}{2}$]2,
∴BQ=9-3$\sqrt{3}$.
即:当PA=EA的等腰三角形时,BQ=0,当EA=EP的等腰三角形时,BQ=9-3$\sqrt{3}$.
点评 此题是一次函数的综合题,主要考查了三角形的相似,锐角三角函数,解本题的关键是找到相等关系,就出线段,本题的难点是用反证法判断出AP≠PE.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,-1) | B. | (-2,-1) | C. | (-1,2) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A. | 8米 | B. | 10米 | C. | 13米 | D. | 14米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,4 | B. | -8,14 | C. | -6,6 | D. | -8,-14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
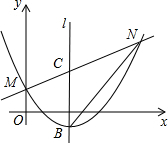 如图,直线y=$\frac{1}{2}$x+1与抛物线y=$\frac{1}{2}$x2-bx+l交于不同的两点M、N(点M在点N的左侧).
如图,直线y=$\frac{1}{2}$x+1与抛物线y=$\frac{1}{2}$x2-bx+l交于不同的两点M、N(点M在点N的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com