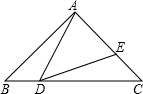
(1)证明:∵△ABC中,∠BAC=90°,AB=AC=1,
∴∠ABC=∠ACB=45°.
∵∠ADE=45°,
∴∠BDA+∠CDE=135°.
又∠BDA+∠BAD=135°,
∴∠BAD=∠CDE.
∴△ABD∽△DCE.
(2)解:∵△ABD∽△DCE,
∴

;
∵BD=x,
∴CD=BC-BD=

-x.
∴
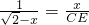
,
∴CE=

x-x
2.
∴AE=AC-CE=1-(

x-x
2)=x
2-

x+1.
即y=x
2-

x+1.
(3)解:∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
又∵△ABD∽△DCE,
∴△ABD≌△DCE.
∴CD=AB=1.
∴BD=

-1.
∵BD=CE,
∴AE=AC-CE=2-

.
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°,
∴此时有∠DEA=90°.
即△ADE为等腰直角三角形.
∴AE=DE=

AC=

.
当AD=EA时,点D与点C重合,不合题意,所以舍去,
因此AE的长为2-

或

.
分析:此题有三问,(1)证明△ABD∽△DCE,已经有∠B=∠C,只需要再找一对角相等就可以了;
(2)由(1)证得△ABD∽△DCE,有相似就线段成比例,于是利用(1)的结果可证得(2);
(3)当△ABD∽△DCE时,可能是DA=DE,也可能是ED=EA,所以要分两种情况证明结论.
点评:此题三个问题各有特点,却又紧密相联,第一个问题考查的是三角形的相似;第二个问题看起来是考查的函数但却与第一问紧密相联,运用第一问的结论即可顺利解决;第三问的关键是分类讨论,要考虑等腰的几种不同情况.

 E点,使∠ADE=45度.
E点,使∠ADE=45度. ;
; -x.
-x.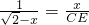 ,
, x-x2.
x-x2. x-x2)=x2-
x-x2)=x2- x+1.
x+1. x+1.
x+1. -1.
-1. .
. AC=
AC= .
. 或
或 .
.

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.