
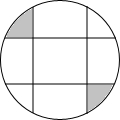
 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π. 分析 根据图形可知圆的面积等于各部分面积之和,再根据每一条弦都将圆分割成面积比为1:3的两个部分列出两个等式,两式联立,求出中间正方形的面积与扇形的面积的关系,再求出中间正方形的面积与它的外接圆面积之比,得到答案.
解答 解:由题意(根据图中假设),设圆的半径为R,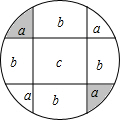
4a+4b+c=πR2①
2a+b=$\frac{1}{4}$πR2 ②
4×②-①得到:c=4a
∵中间这个正方形的面积:这个正方形的外接圆的面积=2;π,
∴这个正方形的外接圆的面积:阴影部分面积=π:1.
故答案为:π.
点评 本题考查的是正多边形与圆的关系,用不同的方式表示圆的面积是解题的关键,还要熟练运用正方形的面积与其外接圆的面积的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
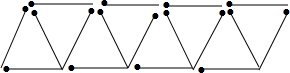 如图所示,用火柴棍拼成一排由三角形组成的图形.
如图所示,用火柴棍拼成一排由三角形组成的图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
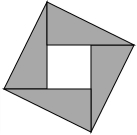 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是4.
如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com