
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的信息,或可以求出一些不规则图形的面积.
(1)如图1所示,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n.观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 .
(2)若图1中每块小长方形的面积为12cm2,四个正方形的面积和为50 cm2,试求图中所有裁剪线(虚线部分)长之和.
(3)将图2中边长为a和b的正方形拼在一起,B,C,G三点在同一条直线上,连接BD和BF,若这两个正方形的边长满足a+b=10,ab=16,请求出阴影部分的面积.

【答案】(1)(1)(m+2n)(2m+n);(2)42cm;(3)26.
【解析】分析:(1)根据图象由长方形面积公式将代数式2m2+5mn+2n2因式分解即可;
(2)根据正方形的面积得出正方形的边长,再利用每块小矩形的面积为12 cm2,得出等式求出m+n,进一步得到图中所有裁剪线(虚线部分)长之和即可.(3) 利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形BGF的面积-三角形ABD的面积求解.
详解:(1)(m+2n)(2m+n)
(2)由题意得:mn=12,2n2+2m2=50,∴n2+m2=25,∴(m+n)2= n2+m2+2mn=49,
∵m>n,∴m+n=7, ∴图中所有裁剪线(虚线部分)长之和=6(m+n)=42(cm)
(3) 阴影部分的面积=0.5a2+b2-0.5b(a+b)=0.5(a2+ b2-ab)=0.5[(a+b) -3ab]=0.5×(100-48)=26.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠1,∠2+∠3=180°.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对面积为s的△ABC逐次进行以下操作:
第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;
第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;
…;
按此规律继续下去,可得到△AnBnCn,则其面积Sn=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过A点分别作两坐标轴的垂线,垂足分别为B、C.
(1)若矩形ABOC的面积为5,求A点坐标.
(2)若点A在线段PQ上移动,求矩形ABOC面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
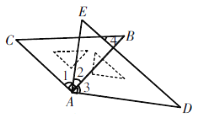
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.


图⑴ 图⑵
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段的中点坐标为![]() .
.
(1)如图(1),C为线段AB中点,A点坐标为(0,4),B点坐标为(5,4),则点C的坐标为
(2)如图(2),F为线段DE中点,D点坐标为(﹣4,﹣3),E点坐标为(1,﹣3).则点F的坐标为________
应用:
(1)如图(3),长方形ONDF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点D的坐标为(4,3),则点M的坐标为 ;
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与A,B,C构成平行四边形的顶点,直接写出D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com