
【题目】已知:△ABC是等边三角形.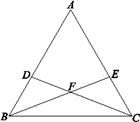
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F. 试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.
【答案】
(1)解:BF=CF;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
在△BCD和△CBE中, 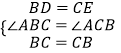 ,
,
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BF=CF.
(2)解:由(1)得:∠BCD=∠CBE,∠ACB=60°,
设∠BCD=∠CBE=x,
∴∠DBF=60°﹣x,
若△BFD是等腰三角形,分三种情况:
①若FD=FB,则∠FBD=∠FDB>∠A,
∴∠FBD=∠FDB>60°,
但∠FBD>∠ABC,
∴∠FBD<60°,
∴FD=FB的情况不存在;
②若DB=DF,则∠FBD=∠BFD=2x,
∴60°﹣x=2x,
解得:x=20°,
∴∠FBD=40°;
③若BD=BF,如图所示: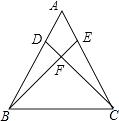
则∠BDF=∠BFD=2x,
在△BDF中,∠DBF+∠BDF+∠BFD=180°,
∴60°﹣x+2x+2x=180°,
解得:x=40°,
∴∠FBD=20°;
综上所述:∠FBD的度数是40°或20°.
【解析】(1)根据题意再由SAS证明△BCD≌△CBE,再由全等三角形的性质可证得结论;
(2)△BFD是等腰三角形,分三种情况:①若FD=FB;②若DB=DF;③若BD=BF,根据三角形的内角和可求出答案.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( )
A.27,25
B.25,27
C.27,27
D.27,30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块长方形铁皮,长100cm,宽50cm,在它的四周各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600cm2 , 设铁皮各角应切去的正方形边长为xcm,则下面所列方程正确的是( )
A.4x2=3600
B.100×50﹣4x2=3600
C.(100﹣x)(50﹣x)=3600
D.(100﹣2x)(50﹣2x)=3600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( ) 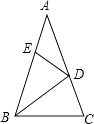
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com