
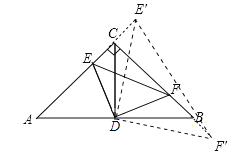
【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

【答案】![]() 或
或![]()
【解析】解:①E在线段AC上.在△ADE和△CDF中,∵AD=CD,∠A=∠DCF,AE=CF,∴△ADE≌△CDF(SAS),∴同理△CDE≌△BDF,∴四边形CEDF面积是△ABC面积的一半.∵CE=1,∴CF=4﹣1=3,∴△CEF的面积=![]() CECF=
CECF=![]() ,∴△DEF的面积=
,∴△DEF的面积=![]() ×
×![]() ×
×![]() ﹣
﹣![]() =
=![]() .
.
②E'在AC延长线上.∵AE'=CF',AC=BC=4,∠ACB=90°,∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=![]() ,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CDCE'cos135°=1+8+2×
,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CDCE'cos135°=1+8+2×![]() ×
×![]() =13,∴S△E'DF'=
=13,∴S△E'DF'=![]() DE'2=
DE'2=![]() .故答案为:
.故答案为: ![]() 或
或![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.

(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.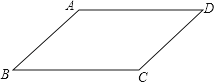
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用数轴解决问题:我们知道,若数轴上点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则
,则![]() 、
、![]() 两点间的距离记作
两点间的距离记作![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() = ;
= ;
(2)若数轴上一点![]() 表示的数是
表示的数是![]() ,
,![]() ,则
,则![]() = ;
= ;
(3)若点![]() 表示的数是
表示的数是![]() ,已知
,已知![]() ,点
,点![]() 在
在![]() 的左边,
的左边,![]() ,点
,点![]() 在点
在点![]() 的右边,
的右边,![]() ,点
,点![]() 以每秒
以每秒![]() 的速度向右移动,同时点
的速度向右移动,同时点![]() 、点
、点![]() 分别以每秒
分别以每秒![]() 、
、![]() 的速度向左移动.设移动时间为
的速度向左移动.设移动时间为![]() 秒,那么
秒,那么![]() 是否有最小值?若有,求出最小值并写出此时
是否有最小值?若有,求出最小值并写出此时![]() 的取值范围;若没有,请说明理由.
的取值范围;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )

A.56° B.66° C.76° D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)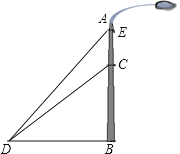
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com