
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.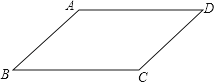
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
【答案】
(1)
BC=DA
(2)
证明:连接AC,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC,
在△ABC和△CDA中, 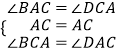 ,
,
∴△ABC≌△CDA(ASA),
∴AB=CD,BC=DA;
故答案为:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC,
在△ABC和△CDA中, 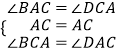 ,
,
∴△ABC≌△CDA(ASA),
∴AB=CD,BC=DA.
【解析】(1)已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA;
故答案为:BC=DA;
本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形对边平行的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:
【题目】如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( ) 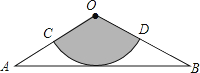
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:
购买商铺后,都由开发商代为租赁10年,10年期满后再由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的5%.
方案二:投资者按商铺标价的八五折一次性付清铺款,4年后每年可以获得的租金为商铺标价的5%,但要缴纳租金的10%作为管理费用.
(1)请问:投资者选择哪种购铺方案,10年后所获得的投资收益率更高?为什么?(注:投资收益率=![]() ×100%)
×100%)
(2)(列方程求解)某投资者按方案一购买商铺,因资金周转,决定向银行贷铺款的20%并于一年后付清贷款,已知贷款年利率为5%.那么10年后该投资者获得55.2万元的收益,问铺款是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这![]() 筐白菜中,最接近
筐白菜中,最接近![]() 千克的那筐白菜为 千克;
千克的那筐白菜为 千克;
(2)若白菜每千克售价![]() 元,则出售这8筐白菜可卖多少元?
元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= ![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= ![]() x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是(
x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ![]() ,1),则点A8的横坐标是 .
,1),则点A8的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点逆时针旋转度得到的,B1的坐标是;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com