
【题目】如图,在ABCD中,AB=2 ![]() cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长cm.
cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长cm.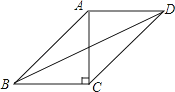
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ;当t=3时,OP=
(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时追上点P?
(3)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时PR相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( ) 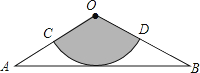
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:
购买商铺后,都由开发商代为租赁10年,10年期满后再由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的5%.
方案二:投资者按商铺标价的八五折一次性付清铺款,4年后每年可以获得的租金为商铺标价的5%,但要缴纳租金的10%作为管理费用.
(1)请问:投资者选择哪种购铺方案,10年后所获得的投资收益率更高?为什么?(注:投资收益率=![]() ×100%)
×100%)
(2)(列方程求解)某投资者按方案一购买商铺,因资金周转,决定向银行贷铺款的20%并于一年后付清贷款,已知贷款年利率为5%.那么10年后该投资者获得55.2万元的收益,问铺款是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com