
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为
【答案】y=x2﹣2x﹣3
【解析】解:∵y=x2+2x+1=(x+1)2 , ∴A点坐标为(﹣1,0),
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,
,
∴点C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
∴C(1,﹣4),
设原抛物线解析式为y=a(x﹣1)2﹣4,
把A(﹣1,0)代入得4a﹣4=0,解得a=1,
∴原抛物线解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.
所以答案是y=x2﹣2x﹣3.
【考点精析】掌握二次函数的性质和抛物线与坐标轴的交点是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】把下面的说理过程补充完整:
已知:如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,并说明理由.

解:∠AED=∠C.
理由:∵∠1+∠ADG=180°(平角定义),∠1+∠2=180°(已知).
∴∠2=∠ADG.(_____________)
∴EF∥AB(______________).
∴∠3=∠AED(_____________).
∵∠3=∠B(已知),
∴∠B=________(________________)
∴DE∥BC(__________________).
∴∠AED=∠C(_________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
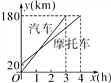
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
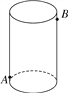
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系 
(1)求该抛物线的解析式.
(2)一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】织里某品牌童装在甲、乙两家门店同时销售A,B两款童装,4月份甲门店销售A款童装60件,B款童装15件,两款童装的销售总额为3600元,乙门店销售A款童装40件,B款童装60件,两款童装的销售总额为4400元.
(1)A款童装和B款童装每件售价各是多少元?
(2)现计划5月将A款童装的销售额增加20%,问B款童装的销售额需增加百分之几,才能使A,B两款童装的销售额之比为4:3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,
, ![]() )].
)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com