
����Ŀ����ͼ��������y=ax2+bx+2��ֱ��l���ڵ�A��B���㣬��A��Ϊ��������y��Ľ��㣬B����2����4���������ߵĶԳ�����ֱ��x=2������A��AC��AB�����������ڵ�C��x���ڵ�D��
��1����������ߵĽ���ʽ��
��2�����D�����ꣻ
��3�����������Ƿ���ڵ�K��ʹ����ACΪ�ߵ�ƽ���ı���ACKL��������ڡ�ABC������������ڣ���ֱ��д����K�ĺ����ꣻ�������ڣ���˵�����ɣ�[��ʾ��������y=ax2+bx+c��a��0���ĶԳ���Ϊx=�� ![]() ����������Ϊ����
�������������� ![]() ��
�� ![]() ��]��
��]��
���𰸡�
��1��
�⣺�߶Գ���Ϊx=2�������߾�����B��
��  ��
��
���ã�a=�� ![]() ��b=2��
��b=2��
�������ߵĽ���ʽ�ǣ�y=�� ![]() x2+2x+2
x2+2x+2
��2��
�⣺�ߵ�A��y���ϣ���x=0����y=2��
���A���꣨0��2����
��BE��y����E��

��AC��AB��AO��OD��
���AOD=��DAO��
�֡ߡ�AOD=��ABE��
���ABE=��DAO��
�ߡ�AEB=��AOD=90�㣬
���ABE�ס�DAO��
�� ![]()
��B����2����4����
��OA=2��AE=6��BE=2��
��OD=6��
���D�����ǣ�6��0��
��3��
�⣺�𣺴����������������ĵ�K��

��AB=2 ![]() ��
��
��S��ABC= ![]() ABAC=Sƽ���ı���ACKL��
ABAC=Sƽ���ı���ACKL��
���K��ֱ��AC����Ϊ ![]() AB=
AB= ![]() ��
��
��ֱ��KL����ʽΪy=�� ![]() x+
x+ ![]() ��
��
�� ![]() x+
x+ ![]() =��
=�� ![]() x2+2x+2��
x2+2x+2��
�����⣻
��ֱ��KL����ʽΪy=�� ![]() x��
x�� ![]() ��
��
�� ![]() x��
x�� ![]() =��
=�� ![]() x2+2x+2��
x2+2x+2��
��ã�x= ![]() ��x=
��x= ![]() ��
��
�����K�㣬������Ϊ ![]() ��
�� ![]()
����������1�����ݶԳ���Ϊֱ��x=2��B���������ϵ㼴�����a��b��ֵ�����ɽ��⣻��2������õ�A���꣬��BE��x����E����֤��ABE�ס�DAO���ɵ� ![]() ���������OD��ֵ�����ɽ��⣻��3�������AB���ȣ��ٸ���S��ABC=
���������OD��ֵ�����ɽ��⣻��3�������AB���ȣ��ٸ���S��ABC= ![]() ABAC=Sƽ���ı���ACKL �� �ɵõ�K��ֱ��AC����Ϊ
ABAC=Sƽ���ı���ACKL �� �ɵõ�K��ֱ��AC����Ϊ ![]() AB�������ֱ��AC����ʽ����ֱ��AC���ϻ�����ƽ��
AB�������ֱ��AC����ʽ����ֱ��AC���ϻ�����ƽ�� ![]() ��λ�����ֱ���������߽��㼴�ɽ��⣮
��λ�����ֱ���������߽��㼴�ɽ��⣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������p��y=ax2+bx+c�Ķ���ΪC����x���ཻ��A��B���㣨��A�ڵ�B��ࣩ����C����x��ĶԳƵ�ΪC�䣬���dz���AΪ�����ҹ���C�䣬�Գ�����y��ƽ�е�������Ϊ������p�ġ���֮�ǡ������ߣ�ֱ��AC��Ϊ������p�ġ���֮�ǡ�ֱ�ߣ���һ�������ߵġ���֮�ǡ������ߺ͡���֮�ǡ�ֱ�߷ֱ���y=x2+2x+1��y=2x+2�������������ߵĽ���ʽΪ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+2��ֱ��l���ڵ�A��B���㣬��A��Ϊ��������y��Ľ��㣬B����2����4���������ߵĶԳ�����ֱ��x=2������A��AC��AB�����������ڵ�C��x���ڵ�D��
��1����������ߵĽ���ʽ��
��2�����D�����ꣻ
��3�����������Ƿ���ڵ�K��ʹ����ACΪ�ߵ�ƽ���ı���ACKL��������ڡ�ABC������������ڣ���ֱ��д����K�ĺ����ꣻ�������ڣ���˵�����ɣ�[��ʾ��������y=ax2+bx+c��a��0���ĶԳ���Ϊx=�� ![]() ����������Ϊ����
�������������� ![]() ��
�� ![]() ��]��
��]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼ҵ�������һ�賧�����Ҷ�������Ҷ����Ϊxǧ�ˣ�x��0�����ܷ���ΪyԪ���������ֹ���ʽ�� ��ʽһ�����̼��������ҽ����11500Ԫ����������Ҷ�۸�Ϊ130Ԫ/ǧ�ˣ����ܷ���=�������ҽ����+�����Ҷ�ѣ�
��ʽ�����ܷ���y��Ԫ���빺���Ҷ����x��ǧ�ˣ��������й�ϵʽ��y= ![]() ��
��
��ش��������⣺
��1��д������ʽһ��y��x�ĺ�����ϵʽ��
��2����������Ҷ����150ǧ�ˣ�˵��ѡ�����ַ�ʽ�����ʡǮ��
��3�����̼Ҳ��÷�ʽһ�������̼Ҳ��÷�ʽ���������̼ҹ������Ҷ400ǧ�ˣ��ܷ��ù���74600Ԫ�������̼ҹ����Ҷ����ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪mΪ��������ʽ��m+2��x2y+mxy2��3x2y�ĺ�Ϊ����ʽ����m��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
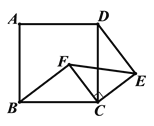
����Ŀ����ͼ���ı���ABCD�������Σ���ECF�ǵ���ֱ�������Σ�����CE=CF�� BC=5��CF=3��BF=4.
��֤��DE��FC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
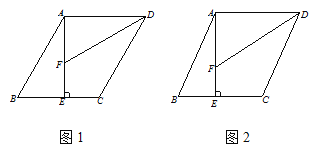
����Ŀ����֪����ABCD�У�AEBC��E��DFƽ��ADC ���߶�AE��F.
��1����ͼ1����AE=AD��ADC=60, ��ֱ��д���߶�CD��AF+BE֮��������ĵ�����ϵ;
��2����ͼ2, ��AE=AD�����ڣ�1���еõ��Ľ����Ƿ���Ȼ����, ������,����Ľ��ۼ���֤��, ��������, ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�س���Ʒѷ�����ͼ��x��km����ʾ��ʻ��̣�y��Ԫ����ʾ���ѣ������ͼ�����������⣺ 
��1���õس��������Ԫ��
��2����x��2ʱ����y��x֮��ĺ�����ϵʽ��
��3����ij�˿���һ�γ˳�������Ϊ18km������λ�˿��踶������Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У�С�����εĶ��������㣬��ABC������������Σ������εĶ��㶼�Ǹ�㣩���밴Ҫ����ɣ�
��1���Ƚ���ABC��ֱ����ƽ��6����λ����ˮƽ����ƽ��3����λ�õ���A1B1C1�����������л�����A1B1C1��
��2������A1B1C1�Ƶ�B1˳ʱ����ת90�����õ���A2B1C2�����������л�����A2B1C2��
��3������ABC��ֱ��B1 C2���ۣ��õ���A3B3C�����������л�����A3B3C��
��4���߶�BC������B��B1�ķ���ƽ�����߶�B1C1�����߶�BCɨ�������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com