
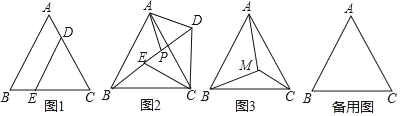
【题目】如图,边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)若将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD,BE,在旋转过程中,AD和BE又怎样的数量关系?并说明理由;
(2)在(1)旋转过程中,边D′E′的中点为P,连接AP,当AP最大时,求AD′的值.
(3)若点M为等边△ABC内一点,且MA=4a,MB=5a,MC=3a,求∠AMC的度数.
【答案】(1)AD'=BE',理由见解析;(2)2![]() ;(3)∠AMC=150°.
;(3)∠AMC=150°.
【解析】试题分析:(1)利用旋转的性质,即可判断出△ACD≌△BCE'即可得出结论;
(2)先判断出点A,C,P三点共线,先求出CP,AP,最后用勾股定理即可得出结论;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,只要证明△CMN是等边三角形,△AMN是Rt△即可解决问题;
试题解析:(1)结论:AD'=BE',
理由:当α≠180°时,由旋转的性质得,∠ACD'=∠BCE',
由(1)知,AC=BC,CD'=CE',
∴△ACD'≌△BCE',
∴AD'=BE';
(2)如图连接CP,
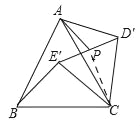
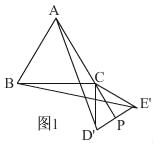
在△ACP中,由三角形三边关系得,AP<AC+CP,
∴当点A,C,P三点共线时,AP最大,
如图1,在△D'CE'中,由P为D'E的中点,得AP⊥D'E',PD'=![]() ,
,
∴CP=3,
∴AP=6+3=9,
在Rt△APD'中,由勾股定理得,AD'=![]() =2
=2![]() ;
;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,
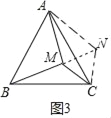
∴CM=CN,BM=AN,△BCM≌△ACN,
∵ABC是等边三角形,
∴∠ACB=60°,
∵∠ACN=∠BCM,
∴∠MCN=60°,
∴△CMN是等边三角形,
∴∠CMN=60°,MN=CM=6,
在△AMN中,∵AM2+MN2=(4a)2+(3a)2=(5a)2=AN2,
∴∠AMN=90°,
∴∠AMC=150°.


科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() 为边
为边![]() 的中点.
的中点. ![]() 是
是![]() 上一点,⊙
上一点,⊙![]() 与
与![]() 相切于点
相切于点![]() ,且与
,且与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .连接
.连接![]() 交
交![]() 于点
于点![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,
, ![]() .当
.当![]() 是⊙
是⊙![]() 的直径时,求
的直径时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达点B为止;点Q以2 cm/s的速度向点D移动。经过长时间P、Q两点之间的距离是10 cm?(8′)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
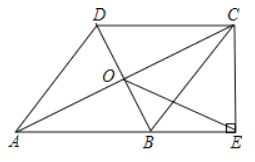
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,在(1)的条件下,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
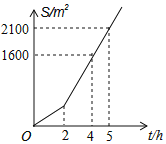
A. 200B. 300C. 400D. 500
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com