
【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为 .
【答案】![]() .
.
【解析】
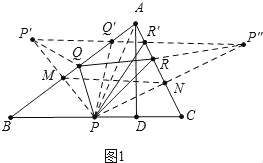
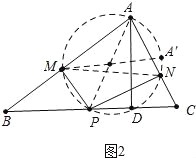
试题分析:如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,此时△PQ′R′的周长最小,这个最小值=P′P″,∵PM=MP′,PN=NP″,∴P′P″=2MN,∴当MN最小时P′P″最小.如图2中,∵∠AMP=∠ANP=90°,∴A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,∵∠MAN是定值,∴直径AP最小时,弦MN最小,∴当点P与点D重合时,PA最小,此时MN最小.如图3中,∵在RT△ABD中,∠ADB=90°,AD=2,DB=3,∴AB=![]() ,在RT△ADC中,∵∠ADC=90°,AD=2,CD=1,∴AC=
,在RT△ADC中,∵∠ADC=90°,AD=2,CD=1,∴AC=![]() ,∵DM⊥AB,DN⊥AC,∴
,∵DM⊥AB,DN⊥AC,∴![]() ACDN=
ACDN=![]() DCAD,∴DN=
DCAD,∴DN=![]() ,AN=
,AN=![]() ,∵∠MAD=∠DAB,∠AMD=∠ADB,∴△AMD∽△ADB,∴
,∵∠MAD=∠DAB,∠AMD=∠ADB,∴△AMD∽△ADB,∴![]() ,∴
,∴![]() =AMAB,同理
=AMAB,同理![]() =ANAC,∴AMAB=ANAC,∴
=ANAC,∴AMAB=ANAC,∴![]() ,∵∠MAN=∠CAB,∴△AMN∽△ACB,∴
,∵∠MAN=∠CAB,∴△AMN∽△ACB,∴![]() ,∴
,∴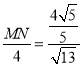 ,∴MN=
,∴MN=![]() ,∴△PQR周长的最小值=P′P″=2MN=
,∴△PQR周长的最小值=P′P″=2MN=![]() .
.
故答案为:![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC不动,将三角板MON绕点O以每秒10°的速度顺时针旋转,旋转时间为t秒 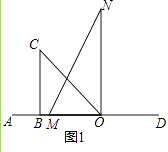
(1)当t=秒时,OM平分∠AOC?如图2,此时∠NOC﹣∠AOM=°; 
(2)继续旋转三角板MON,如图3,使得OM、ON同时在直线OC的右侧,猜想∠NOC与∠AOM有怎样的数量关系?并说明理由; 
(3)若在三角板MON开始旋转的同时,另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转,当OM旋转至射线OD上时同时停止,(自行画图分析)
①当t=秒时,OM平分∠AOC?
(4)②请直接写出在旋转过程中,∠NOC与∠AOM的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
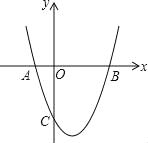
【题目】如图,抛物线y=![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96
B.69
C.66
D.99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2 , 面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是8000元/m2 , 其中厨房可免费赠送 ![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.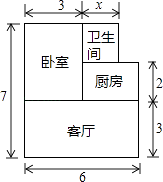
(1)用含x的代数式表示该户型商品房的面积.及方案一、方案二中购买一套该户型商品房的总金额.
(2)当x=2时,哪种方案更优惠?优惠多少元?
(3)张先生因现金不够,于2016年1月在建行借了9万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1250元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.) 假设贷款月利率不变,写出张先生在借款后第n(1≤n≤72,n是正整数)个月的还款数额.(用n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com