Question

【题目】如图，抛物线y=+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．

（1）求抛物线的解析式；

（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，

①试说明EF是圆的直径；

②判断△AEF的形状，并说明理由．

Answer 1

【答案】(1) y=﹣2x﹣3；(2)①证明详见解析；②△AEF是等腰直角三角形，理由详见解析.

【解析】

试题分析：（1）将A、B、C三点坐标代入抛物线方程，即可求得a、b、c的值；

（2）①由B、C、D三点的坐标即可得出∠CBO=∠OBD=45°，从而得出∠EBF=90°，即可得出EF为圆的直径；

②利用同圆内，同弧所对的圆周角相等，可以找到∠AEF=∠AFE=45°，从而得出△AEF是等腰直角三角形．

试题解析：（1）∵抛物线y=+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3），

∴，解得，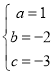

∴抛物线的解析式为y=﹣2x﹣3；

（2）按照题意画出图形，如下图，

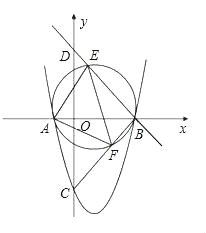
①∵B点坐标（3，0）、C点坐标（0，﹣3），

∴OB=OC=3，

∴△BOC为等腰直角三角形，

∴∠CBO=45°，

又∵D是y轴正半轴上的点，OD=3，

∴△BOD为等腰直接三角形，

∴∠OBD=45°，

∠CBD=∠CBO+∠OBD=45°+45°=90°，

即∠FBE=90°，

∴EF是圆的直径．

②∵∠CBO=∠OBD=45°，∠AFE=∠OBD，∠AEF=∠CBO（在同圆中，同弧所对的圆周角相等），

∴∠AEF=∠AFE=45°，

∴∠FAE=90°，AE=AF，

∴△AEF是等腰直角三角形．